Cours de l’algorithme à l’algorithmique

IREM de LIMOGES
De l'Algorithme…
à
l'Algorithmique …
Formation Continue des enseignants
Nouveaux Programmes de Seconde Juin 2009
Samuel ADABIA
Novembre 2009
Sommaire
Pages
I Notion d'algorithme Définition 3
Exemples d'algorithmes «célèbres» 3
II Forme générale d'un algorithme 4
Premier exemple et problèmes
III Étude des Différentes Parties 6
IV Les Différentes Structures (test , Boucles) 10 à 12
Organigramme
Coût d'un algorithme 12
V Quelques Programmes Simples Pour des algorithmes nouveaux 13
14
VI Analyse d' algorithmes fournis
Algorithme qui ne fonctionne pas Algorithme qui fonctionne mal
Conjecture
VII Algorithme et définition d'une fonction 15
VIII Modification d'algorithme existant pour un résultat nouveau 17
IX De l'algorithme à la programmation Calculatrice 17 X Conclusion 18
XI ANNEXES 19 à 35
Remerciements à Milas FOKLE, Raymond SAURIAT , Bernard DUMORTIER ainsi qu ' Annie
leurs aides. Si vous remarquez des fautes d'orthographes et autres, elles sont de l'entière responsabilité de l'auteur. Vos critiques pour améliorer le document sont les bienvenus à l'Irem auprès de Martine GUERLETIN, formation en algorithmique du 12 nov 2009 ,
I Notion d'algorithme Définition
Activité n°1
Dans une urne on dispose de boules vertes, jaunes, rouges. Soit l'expérience aléatoire qui consiste à tirer une boule de cette urne puis à ranger les boules suivant leur couleur.
Activité n°2
Soit à construire à la règle non graduée et au compas, la médiatrice d'un segment donné.
Dans ces deux activités nous avons mis en œuvre à chaque fois une série d'actions élémentaires qui vont nous conduire au résultat.
Nous dirons tout simplement qu'un algorithme est une succession d'actions menées par étapes et qui permet la réalisation d'une tâche.
Exemple Pour se prémunir contrela grippe A, H1N1, il est recommandé de se laver régulièrement les mains dans la journée. Pour se laver les mains, il faut
- un robinet ou un point d'eau,
- du savon,
- puis il faut ouvrir le robinet,
- se mouiller légèrement les mains,
- se savonner,
- se frotter les mains,
- se les rincer,- fermer le robinet, - s'essuyer les mains.
Comme vous le voyez nous venons de mettre en œuvre un algorithme ( c'est à dire une succession d'actions simples par étapes) qui nous a conduit à nous laver les mains.
Un tel algorithme suscite des interrogations.
Avons-nous toujours à disposition
1)un robinet ou un point d'eau ? Dans le cas contraire que faut il faire ?
2)du savon? Dans le cas contraire que faut-il faire ?
3)un essuie-mains? Dans quel état est-il ? Dans le cas contraire que faut-il faire ?
En conclusion, pour exécuter un algorithme, il est nécessaire que certaines conditions soient réunies, vérifiées, validées. Dans le cas contraire que faut-il envisager ?
Peut-on commencer par se sécher les mains avant de mettre la main sous le robinet ouvert ? La réponse montre de toute évidence que dans un algorithme il s'agit d'une succession d'actions ordonnées exécutées par étapes.
En nous lavant les mains, quand sait-on qu'on sait bien se laver les mains ? qu'on les a lavées suffisamment ? Faut-il continuer ? Jusqu'à quand? Combien de fois dois-je me laver les mains dans la journée? A cette dernière question on s'attend à la réponse : autant que nécessaire, après chaque activité. Toutes ces questions nous amènent à faire des tests, à chercher à boucler ou à terminer ces actions. C'est ce que nous étudierons dans le IV.
Quelques Exemples d'algorithmes « célèbres»
1) L'algorithme d' EUCLIDE permet de d'obtenir le pgcd de deux entiers naturels. Une autre utilisation de cet algorithme a aussi permis d' écrire des fractions continues ou continuées (voir site de l' IREM , fractions continues par Samuel Adabia)
2) L'algorithme de HÖRNER qui permet de factoriser les polynômes de degré inférieur ou égal à 4 plus facilement et plus (mais c'est un peu complexe) par le calcul de coefficients
3) L'algorithme du pivot de GAUSS
pour ne citer que ceux là
II FORME GENERALE D' UN ALGORITHME
Un algorithme se présente en général sous la forme :
Initialisation ou Entrée des données
Ici on récupère les données et/ ou on les initialise
Traitement des données
Ici on effectue les opérations nécessaires pour répondre au problème posé.
Sortie
Ici on affiche le résultat
On peut pour sa clarté ou pour une bonne compréhension de l'algorithme adopter la forme générale suivante:
Déclaration des Variables
Ici on décrit dans le détail les éléments qu'on va utiliser dans l'algorithme
Initialisation ou Entrée des données
Ici on récupère les données et/ ou on les initialise
Traitement des données
Ici on effectue les opérations nécessaires pour répondre au problème posé.
Sortie
Ici on affiche le résultat
Problème n° 1:
Écrire un algorithme permettant de calculer la somme de deux nombres entrés par l'utilisateur. Afficher le résultat
Problème n° 2:
Écrire un algorithme permettant de calculer la moyenne de deux nombres entrés par l'utilisateur. Afficher le
résultat
| Algorithme n°I | Algorithme n°II | Algorithme n°III |
| Variables | Variables | |
| a est le premier nombre | a est le premier nombre | |
| b est le deuxième nombre | b est le deuxième nombre R est le résultat | |
| Initialisations ou Entrée des données | Initialisations ou Entrée des données | Initialisations ou Entrée des données |
| Saisir a | Saisir a | Saisir a |
| Saisir b | Saisir b | Saisir b |
| Traitement des données | Traitement des données | Traitement des données |
| Calculer (a+b)/2 | Calculer (a+b)/2  | R prend la valeur (a+b)/2 |
| Sortie | Sortie | Sortie |
| Afficher le résultat | Afficher le résultat | Afficher la valeur de R. |
Pour un problème aussi simple nous avons pu écrire ou présenter trois algorithmes différents.
Lorsqu'on écrit un algorithme il faut toujours avoir à l'esprit qu'il va être exécuté par une tierce personne qui n'était pas à l'origine de sa création.
Donc il faut envisager tous les cas même ceux qui vous paraîtront les plus farfelus (sans toutefois tomber dans l'excès !).
Pour le problème n°2 voici l'algorithme retenu.
Algorithme n°III
Variables a est le premier nombre
b est le deuxième nombre
R est le résultat
Initialisation ou Entrée des données
Saisir a
Saisir b
Traitement des données
R prend la valeur (a+b)/2
Sortie
Afficher la valeur de R .
Problème n° 3 :
Écrire un algorithme permettant de calculer et d'afficher les coordonnées du milieu de deux points fournis par l'utilisateur.
Problème n° 4 :
Écrire un algorithme permettant de construire au compas et à la règle non graduée la parallèle à une droite D donnée et passant par un point A.
Problème n° 5 :
1) Écrire un seul et même algorithme permettant de calculer et d'afficher le périmètre d'un carré et celui d'un rectangle donnés.
2) Écrire un algorithme permettant de calculer et d'afficher la moyenne pondérée de trois nombres fournis par l'utilisateur.
3) Pour la Classe de première et au delà
Écrire un algorithme permettant de calculer et d'afficher le barycentre de trois points pondérés fournis par l'utilisateur. (la somme de leur poids est non nulle!)
Problème n° 6 :
Écrire un algorithme permettant de résoudre une équation du premier degré à une inconnue.
Problème n° 7:
Écrire un algorithme permettant d' utiliser les critères de divisibilité par 2; 3; 5 ;9 et 11.
Problème n° 8 :
Écrire un algorithme permettant de savoir si le nombre saisi par l'utilisateur est à la fois divisible par 2 et 3.
Problème n° 9:
Écrire un algorithme permettant de résoudre une inéquation du premier degré à une inconnue.
Problème n° 10 : 0n a : 1;1; 2; 3; 5; 8; 13; 21; 34; 55; 89, , Écrire un algorithme puis un programme calculatrice qui permet d'obtenir ces nombres. Les afficher.
III Étude des différentes parties
Les variables
Ce sont des parties de mémoires de la machine (calculatrice ou ordinateur ) qui vont permettre de stocker des données fournies par l'utilisateur ou bien des résultats de calculs. Leur nom doit être simple et leur description claire et compréhensible au premier coup d'œil. Pour être utilisée, chaque variable doit être préalablement déclarée, c'est à dire réservée.
On déclare une variable en lui donnant un nom et en précisant ses caractéristiques(type, taille, ). Notons que cette déclaration est fonction du logiciel qui va interpréter ou faire fonctionner l'algorithme. Par exemple avec ALGOBOX on écrira x est-un-nombre
alors qu'avec le Pascal on dira x : integer; ou bien x : real; et avec LARP dès fois on les déclare dès fois pas
LARP (Logiciel d'Algorithme et Résolution de problèmes ) conçu par Marco LAVOIE. LARP permet de créer très facilement des organigrammes ( de nos jours très peu utilisés)
Pour finir, retenez que la valeur d'une variable n'est pas fixe. Cette valeur change au cours de l'exécution de l'algorithme. Donc si on veut la conserver il faut prévoir une autre variable. En général un tableau fera l'affaire.
Initialisation ou Entrée des données
Ici on crée en fait ce que l'on appelle une interface. La machine demande des informations relatives au problème posé et/ ou on initialise si nécessaire certaines des variables.
Traitement des données
On y rencontre
-les calculs,
-les tests ou structures alternatives, -les structures itératives ou boucle.
Lors des opérations on peut être amené à demander à l'utilisateur de saisir ou de fournir une autre information ( valeur, texte, )
Sortie
On y trouve la ou les réponses au problème posé.
De manière générale, nous utiliserons les deux structures et /ou des combinaisons de celles-ci, lors de l'écriture d'un algorithme en fonction du problème posé.
IV Les Différentes Structures (test, Boucles) , organigramme
Comme structure nous avons
- la structure alternative ou Test qui se présente sous la forme
SI une condition est réalisée ALORS
On exécute un certain nombre d'actions
SINON
On exécute une autre série d'actions FINSI
Certains tests ne nécessitent pas un deuxième traitement. Dans ce cas, on aura la forme ci-dessous:
SI une condition est réalisée ALORS
On exécute un certain nombre d'actions
FINSI
Problème n° 11: Écrire un algorithme qui permet de savoir si le nombre fourni par l'utilisateur est un nombre pair.
Problème n° 12: Écrire un algorithme qui permet de connaître la parité d'un nombre fourni par l'utilisateur.
1)la structure itérative ou boucle Premier cas :
On réalise une action jusqu'à ce qu'une condition soit remplie. Dans ce cas la forme générale est répéter
Une série d'actions
jusqu'àCondition
Problème n° 13 : Écrire un algorithme qui annonce un événement qui aura lieu à une date donnée. Par exemple le 12 novembre 2009 aura lieu la formation algorithmique pour la classe de Seconde.
Deuxième cas :
On a unnombre d' itérations connues à l'avance par exemple faisons tourner une roue 10 fois. ( On prend un compteur de tours de roue ) Dans ce cas la forme générale est
Pour la valeur du compteur allant de 1 à une valeur connue Faire
une série d'actions ou traitement
Fin Pour ( dès qu'on a atteint le nombre prédéfini on sort de la boucle )
Problème n° 14: Écrire un algorithme qui permet d'afficher dix fois le même message.
Troisième cas :
Le nombre d'itérations dépend d'une condition
Tant queune condition est réalisée faire
une série d'actions ou traitement
Fin Tant que(dès que la condition n'est plus réalisée on sort de la boucle )
Problème n° 15
1) Écrire un algorithme permettant d'autoriser l'accès à une information protégée par un code à quatre chiffres
2) Écrire un algorithme qui permet de connaître le nombre de nombres pairs inférieurs ou égaux à un nombre fourni
Remarque :
Quand on regarde très rapidement on se demande pourquoi à la place de la structure
Répéter Tant que
une action on utiliserait pas la structure une action
jusqu'àcondition Fin tant que
En fait il y a une grande différence entre les deux: avec
| Répéter une action jusqu'àcondition | La condition est vérifiée Tant que après chaque exécution du une action traitement alors qu'avec Fin tant que | On vérifie la condition avant chaque exécution. Donc à partir du moment où la condition n'est pas vérifiée on ne peut pas exécuter le traitement |
Une combinaison très souvent rencontrée et aussi source de nombreuses erreurs si mal utilisée est

Tant que un e condition est réaliséefaire
une action
SI une condition est réalisée ALORS
On exécute un certain nombre d'actions
ou traitement
SINON
On exécute une autre série d'actions ou traitement
FINSI
FINTant que
Une autre combinaison souvent rencontrée
Tant que
répéter
une série d'actions jusqu'àCondition
FIN Tant que
Remarques:
1) Lorsqu'on écrit un algorithme, outre le fait qu'il doit être le plus clair possible, on doit à avoir à l'esprit que suivant les logiciels il y a des mots réservés. Un algorithme peut parfaitement fonctionner avec un logiciel et ne pas fonctionner avec un autre non pas parce qu'il est mal conçu mais tout simplement parce que le logiciel interprète autrement les mots.
2) Un algorithme à exécuter c'est une combinaison ou suite d'opérations à effectuer. Suivant la machine chaque opération a un coût prédéfini.
Par exemple on peut convenir qu ' une addition coûtera 0,001 centime d'euros ,une multiplication 0,002 centimes, une soustraction ( ajouter l'opposé) coûtera 0,003 centimes et une division (qui est en fait la multiplication par l'inverse ) coûtera 0,005 centimes d'euros, une affectation coûtera 0,001 centime pour se donner une idée.
C'est ainsi qu'on peut estimer le coût d'un algorithme ou d'un programme.
C'est pour cette raison que très souvent il est indispensable d'optimiser un programme afin de réduire son coût.
COÛT d'un Algorithme
Regardons de plus près avec cet exemple :
Pour i allant de 1 à 2 faire
Pour j allant de 2 à 5 faire p prend la valeur i+j t prend la valeur i*j s prend la valeur i/j
Fin-Pour
Fin-Pour
Quel est le coût de cet algorithme ? Réponse Le coût de cet algorithme est de huit(8) additions + huit(8) multiplications +huit(8) divisions +dix huit(18) affectations
Dans les programmes qui sont la suite logique d'un algorithme, on optimise beaucoup. Ce qui conduit à avoir recours à des procédures , des fonctions, des variables publiques ,des variable privées. Une procédure je dirai est un programme destiné à accomplir une tâche, laquelle servira à un moment précis. Une fonction en générale retourne une valeur qu'il sera utile d'avoir à un moment donné.
Les procédures sont pour un programme ce que sont en général un lemme pour une démonstration. Elles permettent d'avancer.
Dans notre exposé nous ne les avons pas abordées car ces notions sont hors de propos. Il s'agit ici d'élaborer une démarche algorithmique simple et éventuellement programmer ceux-ci.
V Quelques problèmes simples pour des algorithmes nouveaux.
Problème n ° 16
Un immeuble de la région Usselloise comporte six appartements. On se propose de fournir à chaque propriétaire un digicode pour entrer et sortir de l'immeuble. Chaque digicode est composé d'une lettre de l'alphabet choisie parmi «A,E,L,M,S,U» et de quatre entiers naturels obtenus de manière aléatoire.
On précise que les occupants d'un même appartement ont le même code. Écrire un algorithme puis un programme calculatrice répondant au problème posé.
Problème n °17
Un objet repéré par ses coordonnées (cartésiennes) est autorisé à se déplacer de manière aléatoire dans une zone délimitée.
Écrire un algorithme puis un programme calculatrice répondant au problème posé.
Problème n °18
Écrire un algorithme qui permet de dénombrer ou trouver le nombre de fois que l'on a utilisé le chiffre 7 en numérotant les pages d'un livre de 1 à 972.
Ce problème a été trouvé sur le site S.O.S Maths ( http:) et aurait été donné à un élève de sixième !.
Généraliser ce problème de sorte que l'algorithme permette de trouver n'importe quel chiffre (0 à 9 ) utilisé pour écrire les pages d'un livre, le nombre de pages sera demandé. Écrire le programme calculatrice répondant au problème posé.
Problème n °19 Écrire un algorithme qui permet de construire un pentagone régulier. (A ce propos signalons qu'il existe plusieurs méthodes de construction d'un pentagone régulier donc il peut y avoir plusieurs algorithmes)
Problème n °20 (problème ouvert )
François-Louis possède un sac de billes contenant n billes composées de trois couleurs. Bleu, blanc, rouge.
On tire au hasard de ce sac une boule, on note sa couleur puis on la range dans une urne de même couleur. On réitère le processus ainsi de suite jusqu'à vider le sac. Écrire un algorithme qui permet de résoudre le problème posé.
Problème n °21 Écrire un algorithme qui permet de dire si un nombre saisi par l'utilisateur est un nombre triste ou bien un nombre joyeux.
Rappel On dira d'un nombre différent de 1 qu'il est triste si ni la somme des carrés de ses chiffres, ni la somme des carrés des chiffres des nouvelles sommes ainsi obtenues ne donnent jamais 1 . Autrement il est dit joyeux.
Problème n°22 Écrire un algorithme qui permet de dresser la liste de couples de nombres infernaux.
Rappel On dira de deux entiers naturels compris entre 100 et 1000 qu'ils forment un couple de nombres infernaux si la somme des cubes des chiffres qui composent le premier est égale à la somme des cubes des chiffres qui composent le second.
Remarque : Le Problème n °21 est un bon exercice pour faire la différence entre la somme des carrés et le carré de la somme.
VI Analyse d'algorithmes fournis
Problème n°23 voici une série d' algorithme à évaluer:
A) Algorithme Variables a est un entier naturel b est un autre entier naturel
S est leur somme
S1 est une combinaison de a et de b R est le rapport entre S1 et S.
Début
Entrer la valeur du premier entier naturel
Entrer la valeur du deuxième entier naturel
S prend la valeur (a+b)
S1 prend la valeur 3a+7b R prend la valeur de S1/S Afficher S, S1, R.
Fin
Question
Tester cet algorithme avec les quatre cas suivants :
1) a=2 ; b=8. 2) a=4,2 ; b=16,8 . 3) a=6,5; b=26. 4) a=0,37 ; b=1,48.
Quelle conjecture pouvez vous formuler?
Tester avec d'autres couples de nombres. Conclure.
B) Algorithme
Déclaration_des_variables
n est un entier naturel // n est le nombre dont on cherche la nature (pair ou impair ) c est un entier naturel // c est la variable dans laquelle on stocke le calcul
Début_algorithme
lire n
c prend la valeur n/2
si c=0 alors Écrire n est un nombre pair sinon Écrire n est un nombre impair Fin_algorithme
Question
1) Exécuter l' algorithme ci-dessus avec deux ou trois valeurs.
2) Cet algorithme fonctionne-t-il ?.
3) Cet algorithme fonctionne-t-il correctement?
Problème n° 24
Exécuter l' organigramme ci-dessus d'un algorithme donné. Conclure
VII Algorithme et Définition d'une fonction
Algorithme
| Initialisation ou Entrée des données Saisir un nombre | Variables |
| Traitement L'élever au carré; Retrancher deux fois le nombre de départ Sortie Afficher le résultat obtenu A | Début_algorithme Choisir un nombre ; L' élever au carré; Retrancher au résultat deux fois le nombre de départ; Afficher le résultat obtenu A |
Fin_algorithme
Problème n° 25
1) Exécuter l' algorithme ci-dessus avec deux ou trois valeurs.
2) Donner la forme algébrique de A pour tout réel x.
Algorithme
| Initialisation ou Entrée des données Saisir un nombre | Variables Début_algorithme Choisir un nombre ; Retrancher 1 à son double ; 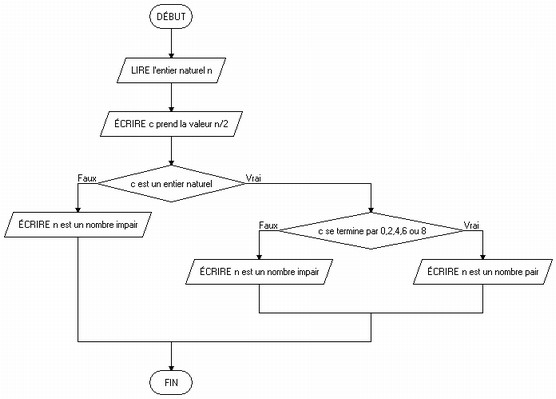 Diviser le résultat par le nombre de départ augmenté de 1; Afficher le résultat obtenu A Fin_algorithme |
| Traitement Retrancher 1 à son double; Diviser le résultat par le nombre de départ augmenté de 1; | |
| Sortie Afficher le résultat obtenu A |
Problème n° 26
1) Exécuter l' algorithme ci-dessus avec deux ou trois valeurs. 2) Donner la forme algébrique de A pour tout x réel donné.
Algorithme
Déclaration
Début
x est un réel
Si x > 0 Alors retrancher 5 à son double écrire le résultat f(x) Sinon
l'élever au carré
lui ajouter le triple du nombre de départ retrancher 7 au résultat écrire le résultat f(x)
Fin si
Fin_algorithme
Problème n° 27
1) Exécuter l' algorithme ci-dessus avec deux ou trois valeurs.
2) Donner la forme algébrique de f(x) pour tout x réel donné
Dorénavant nous adopterons la forme classique suivante pour un algorithme à savoir
Déclaration des variables variable 1
variable 2 ….
Début_algorithme action
action
TEST
action
action
BOUCLE
action
…
Fin_ algorithme
VIII Modification d'algorithme existant pour un résultat nouveau
Problème n° 28 Modif_algo n° 1 :
Modifier l' algorithme du problème n° 25 de façon à obtenir A= x² +4x+5.
Problème n° 29 Modif_algo n° 2 :
Modifier l' algorithme du problème n° 26 de façon à obtenir A= (2x²+1)/(5-x).
Problème n° 30 Modif_algo n° 3 :
1)
Modifier l' algorithme n°2 du problème n° 5 afin de calculer la somme de tous les entiers pairs inférieurs ou égaux à un nombre fourni par l'utilisateur. Afficher cette somme ainsi que leur nombre.
2)
Modifier l'algorithme n°3 du problème n° 5 pour pouvoir déterminer les coordonnées du barycentre d'un système de n points pondérés.
Problème n° 31 Modif_algo n° 4 :
Modifier l' algorithme du problème n° 8 afin de trouver puis d'afficher de tous les entiers multiples de 7 utilisés lorsqu'on a numéroté un livre de 1 à un nombre fourni par l'utilisateur.
Problème n° 32 Modif_algo n° 4 :
Modifier l' algorithme du problème n°10) afin de trouver puis d'afficher de tous les nombres de Fibonacci qui sont premiers et inférieurs à 10000.
Pour terminer on pourra fournir un algorithme écrit sous la forme conventionnelle ou classique et demander à ce que l'on <<reconnaisse>> les trois parties à savoir
1) l'initialisation ou entrée des données 2) le traitement 3) la sortie.
IX De l'Algorithme à la programmation Calculatrice
Tous les programmes écrits ici suite à un algorithme sont adaptables facilement sur les autres types de calculatrices et dans les différents langages étudiés dans le supérieur
Rappelons très rapidement que dans les années 50, les langages utilisés étaient le FORTRAN et le COBOL.
Le Pascal et l' ALGOL ont vu le jour dans les années 60, suivis dans les années 70 par les langages C et ADA puis dans les années 80, le C++ et MATLAB ont fait leur apparition. Des années 90 à nos jours on peut citer Java , Python, XCAS.
De nombreux logiciels permettent de tester un algorithme entre autres citons les logiciels libres LARP (Logiciel d'Algorithme et de Résolution de Problèmes) quelques soucis signalés sur le forum de Marco Lavoie et AlgoBox (logiciel conçu par Pascal Brachet, professeur au lycée Bernard Palissy à AGEN)
Comme souligné ci dessus pour chaque langage, il y a des mots réservés, spécifiques, d'où la nécessité d'avoir un minimum de connaissances sur le langage choisi. Dans un premier temps de simples programmes les autres viendront par la suite.
Dans un programme, l'utilisateur dialogue avec la calculatrice. Pour cela la calculatrice lui demande un certain nombre d'information
Gérer les entrées sorties.
Sur la T.I. 83 plus SE ou bien d'autres , Après chaque opération il faut la valider en appuyant sur ENTER
On rentre en mode programme (soit pour l' EXECuter, soit pour l'EDITer, soit pour l'EFFacer ) en appuyant sur PRGM puis on choisit un nom de programme par exemple algorit (Attention le nombre de lettres autorisées est limité) puis on valide
En gros il y a actions que nous allons utiliser.
1) La calculatrice va poser une question ou bien formuler une demande à l'utilisateur ou afficher une information, un résultat :
Pour cela on dispose de DISP que l'on peut directement écrire à l'aide du clavier ALPHA numérique ou bien que l'on trouve dans PRGM I /O 2 .
Ainsi pour que la calculatrice demande à l'utilisateur de saisir son nom ,un nombre, ,
On écrira :DISP'' merci de saisir votre nom'' ou bien
:DISP'' Veuillez saisir le nombre de pages à écrire''
2) Une fois que l'information a été saisie il faut que la calculatrice la lise. Pour cela on dispose de
INPUT
que l'on peut directement écrire à l'aide du clavier ALPHA numérique ou bien que l'on trouve dans PRGM I /O 3 .
| ? |
3) Lors des calculs il sera nécessaire de mémoriser des résultats, des informations ou bien d'incrémenter un compteur (c'est augmenter celui-ci de 1 ) . Pour cela on dispose de STO que l'on peut directement écrire à l'aide du clavier ALPHA numérique ou bien que l'on trouve sur le clavier principal (avant dernière touche de la 1 ère colonne)
4) On dispose aussi de OUTPUT , on peut sous certaines conditions les combiner.
5) Pour les opérations classiques de calcul nous disposons de fonctions telles que iPART partie entière ou Fpart partie fractionnaire, ALEATOIRE (générateur de nombres aléatoires),ect.
Et sur CASIO
Dans un programme, l'utilisateur dialogue avec la calculatrice. Pour cela la calculatrice lui demande un certain nombre d'information. Chez CASIO çà se fait de la façon suivante: ? ? X, T : avec cette séquence la calculatrice va demander à l'utilisateur d'entrer ou de saisir la valeur de l'inconnue X:
Seul souci c'est qu'il n' y aura pas de nom de variable affiché.
Pour afficher le nom de la variable, on peut procéder ainsi '' X'' cette instruction permet d'afficher du texte. ? ? X, T : 4 X, T EXE , permet de calculer le périmètre d'un carré dont le côté est fourni
| ? | ? | X,T | : | 4 | X,T | EXE |
| ? | ? | X,T | : | X,T | x² | EXE |
Ces deux instructions l'une à la suite de l'autre est un programme. Dans ce même programme on calcule à la fois le périmètre et l'aire d'un carré dont le côté a été fourni.
Problème n° 33 :
Écrire un programme qui demande à l'utilisateur son prénom et lui retourne Bonjour avec ce prénom et lui souhaite la bienvenue.
Problème n° 34:
Écrire le programme calculatrice correspondant à l'algorithme du problème n° 5 -1)
Problème n° 35:
Écrire le programme calculatrice correspondant à l'algorithme du problème n°7 Problème n°36 :

Écrire le programme calculatrice correspondant à l'algorithme du problème n°8 Problème n°37 :
Écrire le programme calculatrice correspondant à l'algorithme du problème n° 10 Problème n°38 :
Écrire le programme calculatrice correspondant à l'algorithme du problème n°17 Problème n°39 :
Écrire le programme calculatrice correspondant à l'algorithme du problème n° 18 Problème n° 40 :
Écrire le programme calculatrice correspondant à l'algorithme du problème n° 20 Problème n° 41:
crire le programme calculatrice correspondant à l'algorithme du problème n° 21 Problème n° 42:
:Écrire le programme calculatrice correspondant à l'algorithme du problème n° 22
Conclusion :
Ce fascicule a pour but d'exposer en des termes clairs la notion d'algorithme, notion liée à l'existence même de l'Homme. Les exemples sont simples pour que tout un chacun puisse s'approprier très rapidement
la notion et être capable : - d'écrire en langage naturel l'algorithme de petits problèmes,
- d'évaluer ou tester des algorithmes fournis,
- de modifier des algorithmes pour qu'ils donnent le résultats souhaités ou pour de nouveaux résultats
puis lorsqu'il est nécessaire passer à la programmation de ceux-ci.
Ce travail a été l'occasion de redécouvrir ou de couvrir de nouvelles notions exploitables dans nos enseignements. L'algorithmique devrait permettre d'éviter l'automaticité et ouvrir la voie de la recherche de la meilleure solution pou un problème donné
ANNEXES
Éléments de correction Problème n°1
Déclaration des variables
a est le premier nombre b est le deuxième nombre R est le résultat
Début_algorithme
Saisir a
Saisir b
R prend la valeur (a+b)
Afficher ''la somme est'', R.
Fin_ algorithme
Éléments de correction Problème n°2 : Donnés à la page 5
Éléments de correction Problème n°3
Le problème n° 3 utilise l'algorithme combiné des problèmes 1 et 2. Calculer le milieu de deux points revient à calculer la moyenne des deux abscisses puis la moyenne des deux ordonnées. On affiche deux résultats au lieu d'un seul dans les problèmes précédents
A vous maintenant Entrée ou Initiations des données
Saisir les coordonnées du 1er point; Saisir les coordonnées du 2ieme point ;
Traitement des informations
Calculer la moyenne des abscisses;
Conserver le résultat dans une variable;
Calculer la moyenne des ordonnées;
Conserver le résultat dans une 2ième variable
Sortie
Afficher le contenu de la 1ère variable;
Afficher le contenu de la 2ième variable
Éléments de correction Problème n°4 construction de parallèle
Variables
Début
lire la position du point A
Si A est sur la droite donnée Alors
Écrire la droite est la parallèle cherchée Sinon
Construire un arc de cercle de centre A qui coupe la droite en deux points B et C.
Construire un arc de cercle de centre A et de rayon BC;
Construire un arc de cercle de centre B et de rayon AC; Nommer D l'intersection des deux arcs.
(AD ) est la parallèle cherchée.
Fin si Fin
Éléments de correction Problème n°5 - 1)
Déclaration des variables
l est un entier naturel // l est la largeur du rectangle l1 est un entier naturel // l1 est la longueur du rectangle
c est un entier naturel // c est le côté du carré p est un entier naturel // p est le périmètre du rectangle q est un entier naturel // q est le périmètre du carré
Début_algorithme
saisir la mesure du côté du carré c prend la valeur de la mesure du côté du carré q prend la valeur quatre fois la mesure du côté du carré saisir la mesure de la largeur du rectangle l prend la valeur de la mesure de la largeur du rectangle saisir la mesure de la longueur du rectangle
l1 prend la valeur de la mesure de la longueur du rectangle
p prend la valeur le double de ( l+l1 ) Afficher '' le périmètre du carré est '' , q
Afficher '' le périmètre du rectangle est '' , p
Fin_ algorithme
Éléments de correction Problème n°5 - 2) Calcul de la moyenne pondérée de trois nombres
A vous maintenant Entrée ou Initiations des données
Saisir la valeur du 1er nombre; saisir son coefficient
Saisir la valeur du 2ieme nombre ; saisir son coefficient
Saisir la valeur du 3ième nombre; saisir son coefficient
Traitement des informations
Calculer le produit de chaque nombre par son coefficient;
Conserver chaque résultat dans une nouvelle variable;
Calculer la moyenne de ces nouveaux nombres;
Conserver le résultat dans une 2ième variable
Sortie
Afficher le contenu de la 2ième variable;
Éléments de correction Problème n°5 - 3)
Calcul du barycentre de trois points pondérés dont la somme des poids est donnée non nulle.
A vous maintenant
Entrée ou Initiations des données
Saisir les coordonnées du 1er point;
Saisir son poids;
Saisir les coordonnées du 2ieme point ;
Saisir son poids;
Saisir les coordonnées du 3ieme point
Saisir son poids;
Traitement des informations
Calculer la moyenne pondérée des abscisses;
Conserver le résultat dans une 1ère variable;
Calculer la moyenne pondérée des ordonnées; Conserver le résultat dans une 2ième variable
Sortie
Afficher le contenu de la 1ère variable;
Afficher le contenu de la 2ième variable
Éléments de correction Problème n°6
Déclaration_des_variables a, b, c et d sont des réels x est un nombre // est l'inconnue
Début_algorithme
saisir a saisir b saisir c saisir d
Tant que ( a ?0 ) ou (c?0) faire
écrire on a bien une équation du premier degré; ajouter à chaque membre l'opposé de b; réduire dans chaque membre;
ajouter à chaque membre l'opposé de cx;
réduire dans chaque membre; Si (a-c) ?0 Alors x prend la valeur (d-b)/(a-c) Sinon Si (d-b)=0 Alors
x prend toutes valeurs réelles Sinon il n'y a pas de solution car la division par zéro. Fin Si Fin Si
Fin Tant que
Afficher '' Il ne s'agit pas d'une équation du premier degré'
Fin_algorithme
Éléments de correction Problème n°8 divisible Éléments de correction Problème n°7 à la fois par 2 et 3
Algorithme programme 7 Déclaration_variables
Les élèves ont eu à travailler sur l'algorithme d'Eu-
clide pour trouver le pgcd de deux nombres. C'est début_algorithme pour çà que nous utilisons dans saisir le nombre
c prend la valeur pgcd de n et 2
Début_algorithme d prend la valeur pgcd de n et 3
saisir un nombre si c=2 et d= 3 alors afficher '' n est divisible à la fois
Si pgcd de n et 2 vaut 2 alors le nombre est divi- par 2 et 3''
sible par 2 finsi
Si pgcd de n et 3 vaut 3 alors le nombre est divi- fin_algorithme sible par 3
Si pgcd de n et 5 vaut 5 alors le nombre est divisible par 5

Si pgcd de n et 7 vaut 7 alors le nombre est divisible par 7
Si pgcd de n et 9 vaut 9 alors le nombre est divisible par 9
Si pgcd de n et 11 vaut 11 alors le nombre est divisible par 11
Fin_algorithme
Éléments de correction Problème n°9
Déclaration_des_variables a, b, c et d sont des réels x est un nombre // est l'inconnue
Début_algorithme
saisir a saisir b saisir c saisir d
Tant que ( a ?0 ) ou (c?0) faire
écrire on a bien une inéquation du premier degré; ajouter à chaque membre l'opposé de b; réduire dans chaque membre;
ajouter à chaque membre l'opposé de cx;
réduire dans chaque membre; Si (a-c) ?0 Alors
si (a-c) >0 alors
afficher '' on conserve le même signe qu'au départ'' x « prend la valeur » (d-b)/(a-c) sinon
afficher '' on change le signe de départ'' x « prend la valeur » (d-b)/(a-c) finsi
Sinon Si (d-b)=0 Alors
x prend toutes valeurs réelles Sinon
afficher '' cela dépend du signe de départ et du signe de (d-b) Fin Si
Fin Si
Fin Tant que
Afficher '' Il ne s'agit pas d'une inéquation du premier degré'' fin_algorithme
Déclaration_des_variables
n est un entier naturel // n est le nombre dont on cherche la nature (pair ou impair ) c est un entier naturel // c est la variable dans laquelle on stocke le calcul
Début_algorithme
lire n
c prend la valeur pgcd de n et 2 si c=2 alors Écrire n est un nombre pair
sinon Écrire n est un nombre impair fin_algorithme
Éléments de correction programme 10 nombres de Fubonacci
Début_algorithme
T (1) prend la valeur 1
T(2) prend la valeur 1
C est un entier
Saisir le nombre n de nombres de Fibonacci cherché
Pour i allant de 1 à n j prend la valeur i-2 k prend la valeur i-1
T(i) prend la valeur T(j)+T(k) fin pour
pour i allant de 1 à n Afficher T('i)
Fin_algorithme
Éléments de correction Problème n°11 et 12
Déclaration_des_variables
n est un entier naturel // n est le nombre dont on cherche la nature (pair ou impair ) s est un entier naturel // s est le compteur de nombre pairs c est un entier naturel // c est la variable dans laquelle on stocke le calcul
Début_algorithme
lire n
c prend la valeur n/2
si c est un entier naturel alors Écrire n est un nombre pair sinon Écrire n est un nombre impair fin_si
fin_algorithme
Éléments de correction Problème n° 13 Éléments de correction Problème n° 14
début_algorithme
répéter début_algorithme
afficher'' stage algorithmique classe de seconde '' Pour i allant de 1 à 10
jusqu'au 12 novembre 2009 afficher '' bon anniversaire''
Fin_algorithme Fin pour
Fin_algorithme
Éléments de correction Problème n° 15-1)
Déclaration des variables
mot_de_passe est une chaine de caractères
Début_algorithme mot_de_passe=''algorithme''
lire le code
Tant que code n'est pas le mot_de_passe lire le code
Fin_tant_que
Afficher '' Félicitations vous avez bien réussi ! ''
Fin_ algorithme
Éléments de correction Problème n° 15-2
Déclaration_des_variables
n est un entier naturel // nous cherchons les nombres pairs inférieurs ou égaux à n
c est un entier naturel // c est la variable dans laquelle on mémorise les calculs intermédiaires p est un entier naturel // p est le compteur de nombres pairs i est un entier naturel // i est le compteur de nombres impairs Début_algorithme
p prend la valeur 0 i prend la valeur 0 lire n j prend la valeur 1
Tant que j < n+1 c prend la valeur pgcd de j et 2 si c=2 alors
p prend la valeur p+1 Écrire j est un nombre pair sinon
i prend la valeur i+1
Écrire j est un nombre impair j prend la valeur j+1 Fin Tant que
afficher '' il y a '' ,p afficher '' nombres pairs'' fin_algorithme
Éléments de correction Problème n ° 16 a lgorithme digicode
Variables
code est un tableau à 6 lignes et 5 colonnes a est un entier naturel
b est un entier naturel Début
a prend une valeur aléatoire entière entre 1 et 6 Si a =1 alors
code(1,1) prend la valeur ' L'
Fin si Si a =2 alors
code(2,1) prend la valeur ' M'
Fin si Si a =3 alors
code(3,1) prend la valeur ' E'
Fin si Si a = 4 alors
code(4,1) prend la valeur ' S'
Fin si Si a =5 alors
code(5,1) prend la valeur ' U' Fin si Si a =6 alors
code(6,1) prend la valeur ' A' Fin si
Pour i allant de 1 à 6 faire Pour j allant de 2 à 5 faire
b prend une valeur aléatoire entière entre 1 et j+4
code(i,j) prend la valeur b
Fin Pour Fin Pour
Afficher les codes
Fin_algorithmique
Éléments de correction Problème n° 17 a lgorithme se déplacer
Variables xmin est un nombre xmax est un nombre ymin est un nombre ymax est un nombre a est un nombre b est un nombre Début xmin prend la valeur -1 xmax prend la valeur 7 ymin prend la valeur -1 ymax prend la valeur 7
Saisir les coordonnées du point D a prend une valeur aléatoire entre -1 et 7 b prend une valeur aléatoire entre -1 et 7
Tant que ( xD > xmin et ( xD <xmax ) Faire
Tant que ( yD > ymin) et ( yD < ymax ) Faire
xD prend la valeur xD +a yD prend la valeur yD +b
Afficher xD,yD
Fin Tant que Fin Tant que
Afficher '' le dernier point est '' Afficher xD,yD.
Fin_algorithme

Éléments de correction Problème n°18 Pages d'un livre
Début-algorithme lire une page
Tant qu'il reste une page faire lire le chiffre des unités lire le chiffre des dizaines lire le chiffre des centaines Si le chiffre des unités est 7 alors
incrémenter le compteur // c'est augmenter le compteur de 1 Si le chiffre des dizaines est 7 alors
incrémenter le compteur // c'est augmenter le compteur de 1 Si le chiffre des centaines est 7 alors
incrémenter le compteur // c'est augmenter le compteur de 1 fin_Tant_que
Affiche la valeur du compteur
Fin_algorithme
Éléments de correction Problème n°19 sera traité lors du stage
Éléments de correction Problème n° 20
Début_algorithme u1 prend la valeur 0 u2 prend la valeur 0 u3 prend la valeur 0
saisir n Si n>2 alors
Pour i allant de 1 à n Tirer une boule
c prend la couleur de la boule tirée si c est bleue alors la mettre dans l'urne U1 incrémenter u1 finsi
si c est blanche alors la mettre dans l'urne U2 incrémenter u2 finsi
si c est rouge alors la mettre dans l'urne U3 incrémenter u3 finsi finpour
else
afficher '' il n'y a pas assez de boules dans l'urne'' finsi fin_algorithme
Éléments de correction Problème n° 21 traité lors du stage Éléments de correction Problème n°22 traité lors du stage Éléments de correction Problème n°23 A)
Avec a=2 et b= 8 on trouve S=10 ; S1= 62 de sorte que S1/S =6,2
Avec a=4,2 et b= 16,8 on trouve S=21 ; S1= 130,2 de sorte que S1/S =6,2
Avec a=6,5 et b= 26 on trouve S=32,5 ; S1= 201,5 de sorte que S1/S =6,2
Avec a=0,37 et b= 1,48 on trouve S=1,85 ; S1= 11,47 de sorte que S1/S =6,2
Sur ces quatre exemples on peut dire que S1=6,2S. Mais il suffit de prendre comme exemple a=1 et b= 2. On trouve S=3 ; S1= 17 pour se rendre compte que S1/S est différent de 6,2.
En conclusion il faudra retenir que quelques exemples ou essais et même nombreux ne suffisent pas à démontrer qu'une propriété est vraie pour tous les objets considérés.
Éléments de correction Problème n°23 B)
La valeur zéro ne sera atteinte et ainsi tous les nombres sont des nombres impairs. Ce qui est faux Donc cet algorithme fonctionne mais mal
Éléments de correction Problème n°24
cette fois-ci nous analysons un organigramme. Il existe le nombre 22 a pour moitié 11 qui est un entier naturel et qui ne se termine pas par 0. Et 22 est bien un nombre pair. Donc cet organigramme n'est pas correct Éléments de correction Problème n°25
Avec quelques essais on trouve que la forme algébrique cherchée est: A=x²-2x.
Éléments de correction Problème n°26
Avec quelques essais on trouve que la forme algébrique cherchée est: A=(2x-1)/(x+1)
Éléments de correction Problème n°27
2x-5 si x>0 f(x) = { x²+3x-7 si x <0
Éléments de correction Problème n°28 Variables
x est un réel
Début_algorithme
Choisir un nombre ; l' élever au carré ;
Éléments de correction Problème n°29 Variables
x est un réel
Début_algorithme
Choisir un nombre ;
Augmenter de 1 le double de son carré; Diviser le résultat par 5 diminué du nombre de départ ;
Afficher le résultat obtenu A
lui ajouter quatre fois le nombre de départ augmenté de Fin_algorithme 5;
Afficher le résultat obtenu A
Fin_algorithme
Éléments de correction Problème n°30 Modif-algo n°3
Déclaration_des_variables
n est un entier naturel // nous cherchons les nombres pairs inférieurs ou égaux à n cpt est un entier naturel // cpt contient la somme des nombres pairs
c est un entier naturel // c est la variable dans laquelle on mémorise les calculs intermédiaires p est un entier naturel // p est le compteur de nombres pairs i est un entier naturel // p est le compteur de nombres impairs
Début_algorithme
cpt prend la valeur 0 p prend la valeur 0 i prend la valeur 0 lire n
j prend la valeur 1
Tant que j < n+1 c prend la valeur pgcd de j et 2 si c=2 alors
p prend la valeur p+1 Écrire j est un nombre pair cpt prend la valeur cpt+ j sinon
i prend la valeur i+1
Écrire j est un nombre impair j prend la valeur j+1
Fin tant que
Afficher '' il y a '' ,p
Afficher '' nombres pairs''
Afficher '' la somme des nombres pairs inférieurs ou égaux à'' , n
Afficher '' est'', cpt
Fin_algorithme
Éléments de correction Problème n° algorithme Définition d'une Fonction
Déclaration
Début
x est un réel
Si x > 0 Alors retrancher 1 à son double
écrire le résultat f(x) Sinon l'élever au carré
lui ajouter son quadruple du nombre de départ
retrancher 3 au résultat
écrire le résultat f(x)
Fin si Fin_algorithme
Corrigé
Éléments de correction Problème n° 5-2
Déclaration des variables S est un entier naturel a est un entier naturel a1 est un entier naturel coef est un entier naturel
Début_algorithme
S prend la valeur 0
Saisir le 1er nombre a
Saisir son coefficient a1
S prend la valeur S+ le produit a par a1 coef prend la valeur a1
Saisir le 2e nombre a
Saisir son coefficient a1
S prend la valeur S+ le produit a par a1 coef prend la valeur a1+coef
Saisir le 3e nombre a
Saisir son coefficient a1
S prend la valeur S + le produit a par a1 coef prend la valeur a1+coef
m prend la valeur m/coef Afficher ''la moyenne est :''
Afficher m
Fin_algorithme
PROGRAMME CALCULATRICE TI 83 plus ou TI 92 problème n° 10
| Nom du programme | pb10( ) |
| Prgm | |
| n est le nombre de termes cherché t est le tableau qui contient les termes les deux premières places sont initialisées à 1 on additionne les deux termes précédents pour obtenir le suivant | Disp '' combien de termes '' Prompt n newlist(n) STO t 1 STO t[1] 1 STO t[2] For i,1,n,1 i-2 STO j i-1 STO k t[j]+t[k] STO t[i] EndFor For i,1,n,1 Dsip '' '' , T[i] EndPrgm |
seront compléter lors du stage
PROGRAMME CALCULATRICE TI 83 plus ou TI 92 problème n° 21

| Nom du programme | pb10( ) |
| Prgm | |
| n est le nombre de termes cherché t est le tableau qui contient les termes les deux premières places sont initialisées à 1 on additionne les deux termes précédents pour obtenir le suivant | ClrIo Disp '' Entrer le premier nombre a '' EndPrgm |
PROGRAMME CALCULATRICE TI 83 plus ou TI 92 problème n° 22
| Nom du programme | pb10( ) |
| Prgm | |
| n est le nombre de termes cherché t est le tableau qui contient les termes les deux premières places sont initialisées à 1 on additionne les deux termes précédents pour obtenir le suivant | ClrIo Disp '' Entrer le premier nombre a '' Disp '' Entrer le deuxième nombre b'' For i,100,1000,1 EndFor EndPrgm |
PROGRAMME CALCULATRICE TI 83 plus ou TI 92 problème 20
| Nom du programme | pb20( ) |
| Prgm | |
| uui désigne l'urne n° i on génère un nombre aléatoire entre 1 et 3 On décide que 1 simule la boule bleue, que 2 simule la boule blanche et que 3 simule la boule rouge l'affectation uui+1 STO signifie que l'on met la boule dans l urne correspondante et que compte le nombre de boules dans celleci | 0 STO uu1 0 STO uu2 0 STO uu3 ClrIo Disp''Entrer le nombre de boules '' prompt n If n > 2 Then For i,1,n,1 int(1+3*rand()) STO j If j =1 then Afficher'' on a une boule bleue'' EndIf uu1+1 STO uu1 If j =2 then Afficher'' on a une boule blanche'' EndIf uu2+1 STO uu2 If j =3 then Afficher'' on a une boule rouge'' EndIf uu3+1 STO uu3 EndFor ClrIo Output 2,10,'' l urne contient '' Output 2,105, uu1 Output 2,125, '' boules bleues'' Output 30,10,'' l urne contient '' Output 30, 105, uu2 Output 30,125, '' boules blanches'' Output 50,10,'' l urne contient '' Output 50,105, uu1 Output 50,125, '' boules rouges'' Else Dsip ''il n' y a pas assez de boules dans l urne '' EndIf EndPrgm |
Éléments de correction Problème 18 Pages d'un Livre
| Nom du programme | Page72( ) |
| i est le numéro de la page que l'on écrit s est le compteur des unités m est le compteur des dizaines t est compteur des centaines a est le nombre du chiffre cherché | Prgm 0 STO i 0 STO s 0 STO m 0 STO t 0 STO a |
| n est le nombre de pages à écrire Le Mod donne le reste de la division euclidienne de a par b iPart donne le quotient entier | Prompt n Input '' quel est le chiffre cherché '',z While i<n+1 mod(i,10) STO u mod(iPart(i/10),10) STO d iPart(i/10) STO c If u=z Then s+1 STO s EndIf If d=z Then m +1 STO m EndIf If u=z Then t+1 STO t EndIf i+1 STO i EndWhile s+m+t STO a Disp '' il y a '', s Disp '' unités de'' ,z Disp '' il y a '', m Disp '' dizaines de'' ,z Disp '' il y a '', t Disp '' centaines de'' ,z Disp'' on a utilisé en tout '' , a Disp'' fois le chiffre '',z disp'' pour numéroter les pages de 1 à '' , n EndPrgm |
Quelques documents à consulter :
1) Ressources pour la classe de Seconde – Algorithmique 2) d'algorithmique par Christophe Darmangeat Université 3) Cours d'algorithmique Iut-Orsay.
4) de la pierre à la puce E. BARBIN
