Exercice Algorithme : Les Tableaux - Le Tri - Les Fichiers

Exercice (1) : Les Tbleaux
1/
Ecrivez un algorithme qui permette la saisie d’un nombre quelconque de valeurs, sur le principe de l’ex 8 (dans la série Les Tableau (Partie 2)). Toutes les valeurs doivent être ensuite augmentées de 1, et le nouveau tableau sera affiché à l’écran:
2/
Ecrivez un algorithme permettant, toujours sur le même principe, à l’utilisateur de saisir un nombre déterminé de valeurs. Le programme, une fois la saisie terminée, renvoie la plus grande valeur en précisant quelle position elle occupe dans le tableau. On prendra soin d’effectuer la saisie dans un premier temps, et la recherche de la plus grande valeur du tableau dans un second temps.
3/
Toujours et encore sur le même principe, écrivez un algorithme permettant, à l’utilisateur de saisir les notes d'une classe. Le programme, une fois la saisie terminée, renvoie le nombre de ces notes supérieures à la moyenne
Solution
1/
Variables i, j, N1, N2, S en Numérique
Tableaux T1(), T2() en Numérique
Debut
… On ne programme pas la saisie des tableaux T1 et T2.
On suppose que T1 possède N1 éléments, et que T2 en possède T2)
…
S ? 0
Pour i ? 0 à N1 – 1
Pour j ? 0 à N2 – 1
S ? S + T1(i) * T2(j)
j Suivant
i Suivant
Ecrire "Le schtroumpf est : ", S
Fin
2/
Variables Nb, i en Numérique
Tableau T() en Numérique
Debut
Ecrire "Entrez le nombre de valeurs : "
Lire Nb
Redim T(Nb-1)
Pour i ? 0 à Nb - 1
Ecrire "Entrez le nombre n° ", i + 1
Lire T(i)
i Suivant
Ecrire "Nouveau tableau : "
Pour i ? 0 à Nb – 1
T(i) ? T(i) + 1
Ecrire T(i)
i Suivant
Fin
3/
Variables Nb, Posmaxi en Numérique
Tableau T() en Numérique
Ecrire "Entrez le nombre de valeurs :"
Lire Nb
Redim T(Nb-1)
Pour i ? 0 à Nb - 1
Ecrire "Entrez le nombre n° ", i + 1
Lire T(i)
i Suivant
Posmaxi ? 0
Pour i ? 0 à Nb - 1
Si T(i) > T(Posmaxi) alors
Posmaxi ? i
Finsi
i Suivant
Ecrire "Element le plus grand : ", T(Posmaxi)
Ecrire "Position de cet élément : ", Posmaxi
Fin
4/
Variables Nb, i, Som, Moy, Nbsup en Numérique
Tableau T() en Numérique
Debut
Ecrire "Entrez le nombre de notes à saisir : "
Lire Nb
Redim T(Nb-1)
Pour i ? 0 à Nb - 1
Ecrire "Entrez le nombre n° ", i + 1
Lire T(i)
i Suivant
Som ? 0
Pour i ? 0 à Nb - 1
Som ? Som + T(i)
i Suivant
Moy ? Som / Nb
NbSup ? 0
Pour i ? 0 à Nb - 1
Si T(i) > Moy Alors
NbSup ? NbSup + 1
FinSi
i Suivant
Ecrire NbSup, " élèves dépassent la moyenne de la classe"
Fin
Exercice (2) : Les Tableaux (Recherche)
Objectif : Testez vos connaissances dans le domaine d'Algorithmique.
Travail à Faire:
Ecrire les Algorithmes permettant de répondre aux questions suivantes :
- Recherche du plus grand élément d'un tableau
- Existence d'un élément dans un tableau
- Recherche d'une valeur dans un tableau
- Recherche du nombre d'occurrences dans un tableau
Solution :
1. Recherche du plus grand élément d'un tableau :
Algorithme Maximum (t : tableau d'entiers ; n : entier)
{Recherche l'élément le plus grand d'un tableau de taille n non nulle}
Lexique i, max : entier
Début
Max = t [1]
Pour i = 2 à n faire
Si (t[i] > max)
Alors max = t[i]
Fin si
Fin Pour
Afficher
2. Existence d'un élément dans un tableau :
Algorithme Présent (e : entier ; t : tableau d'entiers ; n : entier)
{Indique si l'élément e est présent ou non dans le tableau t }
Lexique i : entier
Début
i = 1;
Tant que (i <= n) et non(t[i] = e) faire
i = i+1
Fin tant que
Si (i>n)
Alors Afficher ("l'élément recherché n'est pas présent")
Sinon Afficher ("l'élément recherché a été découvert")
Fin si
Fin
3. Recherche d'une valeur dans un tableau :
t[N] : Tableau d'Entier
v : Entier
i, indice : Entier
trouve : Booleen;
trouve := FAUX
indice = -1
i = 0
tant que non trouve ET i <= N
si t[i] = v alors
trouve = true
indice = i
sinon
i = i+1
finsi
fin tant que
4. Recherche du nombre d'occurrences dans un Tableau :
t[N] : Tableau d'Entier
v : Entier
i, nb : Entier
nb = 0
pour i de 1 à N
si t[i] = v alors
nb := nb+1
finsi
fin pour
Exercice (3) : Le PGCD
Enoncé de l'Exercice:
Donner l’algorithme qui calcule le PGDC (plus grand diviseur commun).
Exemple : calcul du PGDC des deux nombres 1000 et 24
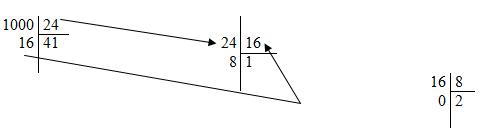
On continue jusqu'à avoir un reste nul. Le dernier nombre, par lequel on a divisé, est le PGDC. Ainsi, le PGDC est égal à 8.
Pour plus de Simplicité :
À chaque ligne suivante:
- A prend la valeur de B,
- B celle de R.
Et, on recommence la division avec ces nouvelles valeurs de B et R.
On s'arrête lorsque R est nul.
Le PGCD est égal au B final.
Solution :
Première Solution:
Fonction Euclide( u : entier v : entier) : entier
Variables
r : entier (* le reste d'une division entière *)
Début
Tant que v 0 faire
r = u mod v
u = v
v = r
Fin Tant que
retourner u
Fin
Variables
u,v : entier (* les deux entiers donnés par l'utilisateur *)
Début
Écrire("Donner les deux nombres : ")
Lire(u,v)
(* Début question subsidiaire *)
si u=0 et v=0 alors Écrire("Le PGCD n'existe pas")
sinon début
si u < 0 alors u := -u
si v < 0 alors v := -v
Écrire(euclide(u,v))
fin
Fin
Deuxième Solution:
Var a, b, PGCD ; Entier Ecrire "Introduisez le 1er nombre: " lire a Ecrire "Introduisez le 2ème nombre: " lire b
tant que NOT (a*b=0) faire selon que 1: a mod 2+b mod 2=0 faire PGCD Ecrire "PGCD = ", PGCD*b sinon écrire "PGCD = ", PGCD*a fin si
Exercice (4) : Palindrome
Enoncé de l'Exercice:
Un palindrome est un tableau de caractères qui se lit de la même façon dans les deux sens (ex : « elle »,« radar », « laval »).
La fonction doit renvoyer 1 si le tableau est un palindrome et 0 sinon.
- Écrire une fonction qui dit si un tableau est un palindrome.
- Écrire la même fonction mais cette fois-ci en ajoutant la possibilité d'avoir des espaces et des apostrophesdans le palindrome (ex : « tu l'as trop ecrase Cesar ce port salut »)
- Ecrire une Fonction qui teste si un mot est un palindrome.
Solution :
1. Écrire une fonction qui dit si un tableau est un palindrome.
Entier palindrome (entier T[],entier taille)
{
Entier i, j
i= 0
j= taille-1
Tant que i<= j faire
Si T[i] =T[j]alors
renvoyer0
Sinon
i = i+1
j = j-1
Fin si
Fin tant que
renvoyer1
}
2. Écrire la même fonction mais cette fois-ci en ajoutant la possibilité d'avoir des espaces et des apostrophesdans le palindrome (ex : « tu l'as trop ecrase Cesar ce port salut »)
Entier Palindrome(entier T[], entier taille)
{
Entier i, j
I = 0
J = taille-1
Tant que i<= j faire
Si T[i]=’ ’alors
i = i+1
Sinon
Si T[j] ==’ ’alors
j= j-1
Sinon
Si T[i] =T[j]alors
renvoyer0
Sinon
i =i+1
j =j-1
Fin si
Fin si
Fin si
i = i+1
j = j-1
Fin tant que
renvoyer1
}
3. Ecrire l'Algorithme qui teste si un mot est un palindrome.
function palindrome(s: string): boolean;
begin
if length(s) < 2 then
palindrome := true
else
if (s[1] = s[length(s)]) then
palindrome := palindrome(copy(s, 2, length(s) - 2))
else
palindrome := false;
end;
Exercice (5) : Les Tableaux (Calcule)
Enoncé de l'Exercice:
Ecrire les Algorithmes permettant de faire :
1. Le calcul du produit scalaire de deux vecteurs réels u et v de dimension

2. Ecrire l’algorithme qui calcule le produit de deux matrices carrées réelles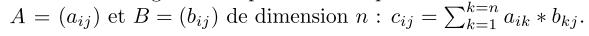
3. Ecrire un algorithme qui calcule le plus grand écart dans un tableau (l’écart est la valeur absolue de la déférence de deux éléments).
4. Le calcul de la moyenne et du minimum des éléments d’un tableau
Solution :
1. Le calcul du produit scalaire de deux vecteurs réels u et v de dimension

Produit_scalaire (u: Tableau d’entiers, v: Tableau d’entiers n:entier):entier
VAR i, prod_scalaire : entiers
Début
prod_scalaire
Pour i
prod_scalaire
Fin pour
Retourner prod_scalaire;
Fin
2. Ecrire l’algorithme qui calcule le produit de deux matrices carrées réelles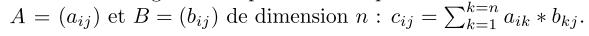
Produit_matriciel (a: Matrice carrée, b: Matrice carrée, n: entier): Matrice carrée
VAR c: Matrice carrée *n
i: entier
Début
Pour i
Pour j de 1 a n Faire
c[i][j]
Pour k de 1 a n Faire
c[i][j]
Fin pour
Fin pour
Fin pour
Retourner c
Fin
3. Ecrire un algorithme qui calcule le plus grand écart dans un tableau (l’écart est la valeur absolue de la déférence de deux éléments).
VAR : min, max, i: entiers
Début
min = t[1]
max = t[1]
Pour i
Si t[i] > max
Alors
Max = t[i]
Fin si
Si t[i] < min
Alors
Min = t[i]
Fin si
Fin pour
Return max - min
Fin
4. Le calcul de la moyenne et du minimum des éléments d’un tableau
VAR somme, i: entiers
Moyenne : réel
Début
Somme
Pour i
Somme
Fin pour
Moyenne
Retourner Moyenne
Minimum(T: Tableau d’entier, N: entier):entier
VAR min, i: entiers
Début
min
Pour i
Si T[i]<min
Alors min =T[i]
Fin si
Fin pour
Retourner min
Fin
Exercice (6) : Le Tri à Bulles
Enoncé de l'Exercice:
- Réaliser l'Algorithme du Tri à Bulles
Principe de la méthode : Sélectionner le minimum du tableau en parcourant le tableau de la Fin au début et en échangeant tout couple d'éléments consécutifs non ordonnés.
Exemple:

Solution :
Procédure TriBulles (E/S t : Tableau [1..MAX] d'Entiers, nbElements : Naturel) Déclaration i,k : Naturel Début Pour i Pour k si t[k]<t[k-1] alors Echanger(t[k],t[k-1]) Fin si Fin pour Fin pour Fin
Exercice (7) : Le Tri par minimum successif
Enoncé de l'Exercice:
Le Tri par minimum successif
Principe
Le tri par minimum successif est ce que l'on appelle un tri par sélection :
Pour une place donnée, on sélectionne l'élément qui doit y être positionné
De ce fait, si on parcourt la tableau de gauche à droite, on positionne à chaque fois le plus petit élément qui se trouve dans le sous tableau droit
Ou plus généralement : Pour trier le sous-tableau t[i..nbElements] il suffit de positionner au rang i le plus petit élément de ce sous-tableau et de trier le sous-tableau t[i+1..nbElements]
Exemple :
Pour trier101, 115, 30, 63, 47, 20[1], on va avoir les boucles suivantes :
i=1101, 115, 30, 63, 47, 20[1]
i=220, 115, 30, 63, 47, 101[1]
i=320, 30, 115, 63, 47, 101[1]
i=420, 30, 47, 63, 115, 101[1]
i=520,30, 47, 63, 115, 101[1]
Donc en sortie :20, 30, 47, 63, 101, 155[1]
Travail à Faire :
- Créer une fonction qui pour soit capable de déterminer le plus petit élément (en fait l'indice du plus petit élément) d'un tableau à partir d'un certain rang
- Créer l’algorithme du Tri par minimum successif
Solution :
1)
Fonction indiceDuMinimum (t : Tableau[1..MAX] d'Entier ; rang, nbElements : Naturel) : Naturel
Déclaration i, indiceCherche : Naturel
Début
indiceCherche
Pour i
si t[i]<t[indiceCherche] alors
indiceCherche
Fin si
Retourner indiceCherche
Fin pour
Fin
2)
L'algorithme de tri est donc :
procédure effectuerTriParMimimumSuccessif (E/S t : Tableau[1..MAX] d'Entier; E nbElements : Naturel)
Déclaration i,indice : Naturel
Début
Pour i
Indice
si i indice alors
echanger(t[i],t[indice])
Fin si
Fin pour
Fin
Exercice (8) : Le Tri Rapide
Principe de la méthode
Choisir un élément du tableau appelé pivot,
Ordonner les éléments du tableau par rapport au pivot
Appeler récursivement le tri sur les parties du tableau à gauche et à droite du pivot.
Travail à Faire :
- Réaliser l’Algorithme du Tri Rapide
Solution :
Procédure TriRapide (E/S t : Tableau [1..MAX] d'Entier; gauche,droit : Naturel) Déclaration i,j : Naturel; pivot,x : Entier Début i j Répéter Tant que t[i] < pivot Faire i Fin tant que Tant que t[j] > pivot Faire j Fin tant que Si i <= j alors Echanger(tab[i],tab[j]) I J Fin si Jusqu'à ce que i > j Si gauche < j alors TriRapide(t, gauche, j) Fin si Si i < droit alors TriRapide(t, i, droit) Fin si Fin
Exercice (9) : calcule la surface d’un rectangle
Exercice (spécifications).
On veut calculer la surface d’un rectangle.
Phase 1 : Étape de réflexion (conception abstraite).
A partir de l'énoncé on doit définir les flux entrants (les données du problème), les flux sortants (les résultats du problème), et le moyen de passer des uns aux autres.
On détermine aisément le résultat il fait partie de l’énoncé (la surface d’un rectangle), ce qui n’est pas le cas des données.
On va donc mettre en place un calcul permettant de déterminer le résultat (de façon simple) ce qui fera apparaître par décomposition fonctionnelle les données indispensables.
Résultat
La surface du rectangle SURF
Traitement
SURF = LONG * LARG
Données
Avec
La longueur du rectangle LONG
La largeur du rectangle LARG
Phase 2 : L'algorithme associé à son lexique (conception concrète).
Lexique
LONG (réel) La longueur du rectangle
LARG (réel) La largeur du rectangle
SURF (réel) La surface du rectangle
Début
Lire(LONG, LARG)
SURF ç LONG * LARG
Ecrire(SURF)
Fin
Exercice (10) : Les Fichiers
Travail à Faire :
- Faire l’algorithme d’une action qui lit un fichier d’entiers et affiche tous les entiers de ce fichier qui sont pairs.
- Ecrire une action qui lit un fichier d’entiers et met dans un autre fichier d’entiers les valeurs paires.
- Faire une fonction qui recherche un entier x dans un fichier d’entiers et retourne vrai si x est dans le fichier.
Rappel:
Pour ouvrir un fichier :
OuvrirFichier (IdFic, ModeOuverture)
Avec ModeOuverture = lecture ou écriture ou rajout.
Pour fermer un fichier
FermerFichier (IdFic)
Pour lire un fichier
LireFichier (IdFic, élément) cela correspond à Lire(n) Ù cin>>n
Pour écrire un fichier
EcrireFichier (IdFic, élément) cela correspond à Ecrire(n) Ù cout<<n
Solution :
Action EntierPairs (E : Fic : fichier d’entiers)
Var n : entier
Début
OuvrirFichier (Fic, lecture)
Si EtatFichier (Fic) = succès alors
LireFichier (Fic, n)
Tant que (EtatFichier (Fic) ? FdF) faire {ou FdF signifie Fin de
Fichier}
Si n%2=0 alors Ecrire(n)
LireFichier(n)
FermerFichier (Fic)
Sinon Ecrire (« Erreur, impossible d’ouvrir le fichier en lecture »)
Fin
Action EntiersPairsFichier (E : f1 : fichier d’entiers, ES : f2 : fichier d’entiers)
Var n : entier
Début
OuvrirFichier (f1, lecture)
Si EtatFichier (f1) = succès alors
OuvrirFichier (f2, écriture)
Si EtatFichier (f2) = succès alors
LireFichier (f1, n)
Tant que EtatFichier(f1)?FdF faire
Si n%2=0 alors EcrireFichier(f2, n)
LireFichier (f1, n)
FermerFichier(f2)
Sinon écrire (« Erreur en écriture »)
FermerFichier (f1)
Sinon écrire (« Erreur en lecture »)
Fin
Fonction Recherche (x : entier, f : fichier d’entiers) : booléen
Var bool repÍ false
Début
OuvrirFichier (f, lecture)
Si EtatFichier(f)=succès alors
LireFichier(f, n)
Tant que (EtatFichier(f) ? FdF ET n?x) faire
LireFichier(f, n)
Si n=x alors repÍ true
FermerFichier (f)
Sinon Ecrire (« Erreur en lecture »)
Fin
Exercice (11) : Les Fichiers (suite .)
Travail à Faire :
Faire une action de fusion de deux fichiers d’entiers. Le fichier de sortie doit être trié.
Rappel:
Pour ouvrir un fichier :
OuvrirFichier (IdFic, ModeOuverture)
Avec ModeOuverture = lecture ou écriture ou rajout.
Pour fermer un fichier
FermerFichier (IdFic)
Pour lire un fichier
LireFichier (IdFic, élément) cela correspond à Lire(n) Ù cin>>n
Pour écrire un fichier
EcrireFichier (IdFic, élément) cela correspond à Ecrire(n) Ù cout<n
Solution :
Action Fusion ( E : f1 : fichier d’entiers, E : f2 : fichier d’entiers, S : f3 : fichier d’entiers) Var : f3 : fichier d’entiers
Début
OuvrirFichier (f1, lecture) Si EtatFichier (f1)=succès alors OuvrirFichier (f2, lecture) Si EtatFichier (f2)=succès alors OuvrirFichier (f3, écriture) Si EtatFichier (f3)=succès alors LireFichier (f1, n1) LireFichier (f2, n2) Tant que (EtatFichier(f1) ?FdF ET EtatFichier(f2)?FdF) faire Si n1 EcrireFichier (f3, n1) LireFichier (f1, n1) Sinon EcrireFichier (f3, n2) LireFichier (f2, n2) Si EtatFichier (f1) ? FdF alors Répéter EcrireFichier (f3, n1) LireFichier(f1, n1) Jusqu'à EtatFichier(f1)=FdF Si EtatFichier (f2) ? FdF alors Répéter EcrireFichier (f3, n2) LireFichier (f2, n2) Jusqu'à EtatFichier (f2) = FdF FermerFichier (f3) Sinon écrire (« Erreur en écriture sur le fichier destination ») FermerFichier (f2) Sinon écrire (« Erreur de lecture sur le fichier f2 ») FermerFichier (f1) Sinon écrire (« Erreur en lecture sur le fichier f1 ») Fin
Exercice (12) : Les Fichiers (2)
Soit le type suivant :
Type : Tetd = entité ( Nom : chaîne
Numéro : étudiant
Notes : tableau [5] d’entiers
Moyenne : entier)
On suppose que la fonction de saisie
Fonction SaisieEtd () : Tetd
Permettant de saisir un tableau de Tetd existe. On pourra donc s’en servir
- Ecrire une fonction qui permet de saisir un groupe d’étudiant dans un fichier.
- Ecrire une fonction qui permet de calculer la moyenne générale d’un groupe d’étudiant.
Solution :
Action SaisieGroupe (E : nb : entier, S : Fic : fichier de Tetd) Var : etd : Tetd i : entier
Début
OuvrirFichier (fic, écriture) Si EtatFichier (fic)=succès alors Pour i de 1 à nb faire EtdÍSaisieEtd( ) EcrireFichier (fic, etd) FermerFichier (fic) Sinon écrire (« Erreur ») Fin Fonction Moyenne (fic : fichier de Tetd ) : réel Var : Som : réel
Début
SomÍ0 nbÍ 0 OuvrirFichier (fic, lecture) Si EtatFichier (fic)=succès alors LireFichier (fic, etd) Tant que EtatFichier (fic)?FdF) faire nbÍnb+1 SomÍSom + etd.moyenne LireFichier(fic, etd) Retourner (Som/nb) FermerFichier (fic) Sinon écrire (« Erreur ») Fin
