Tutoriel Excel : Coefficient de corrélation
Rédigé par Hanane Mouqqadim, Publié le 29 Mars 2019, Mise à jour le Lundi, 28 Décembre 2020 18:54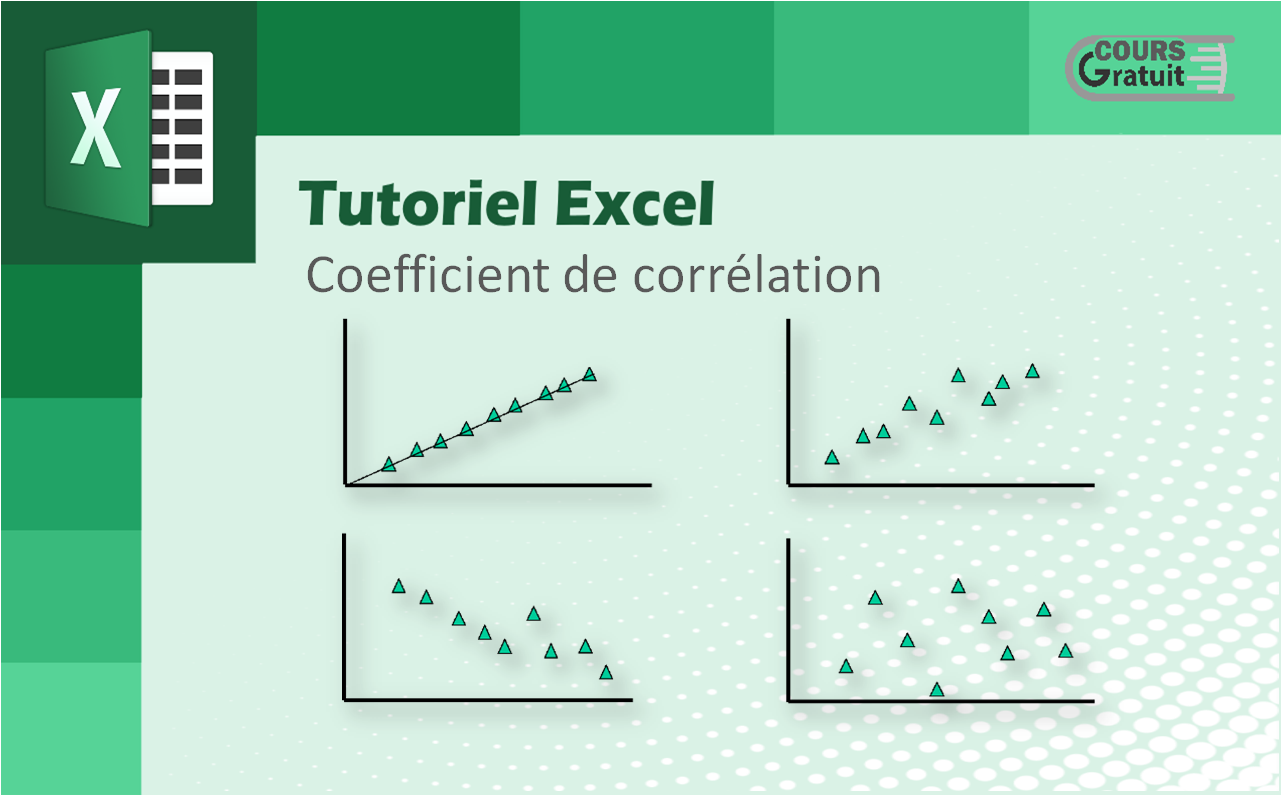
L'un des calculs statistiques d’Excel les plus simples et les plus courants que vous puissiez effectuer est la corrélation. C’est une statistique simple, mais elle peut être très informative lorsque vous voulez savoir si deux variables sont liées. Si vous connaissez les bonnes commandes, trouver le coefficient de corrélation dans Excel est extrêmement facile.
Nous examinerons la corrélation pour vous donner une idée des informations qu’elle vous fournit. Nous allons ensuite rechercher le coefficient de corrélation dans Excel en utilisant deux méthodes et un bon graphique pour examiner les corrélations. Enfin, je vous donnerai une introduction très rapide à la régression linéaire, une autre fonction statistique qui pourrait s’avérer utile lorsque vous examinez les corrélations.
Ce tutoriel explique les bases de la corrélation dans Excel, montre comment calculer un coefficient de corrélation, construire une matrice de corrélation et interpréter les résultats. Bien que simple, la corrélation est très utile pour comprendre les relations entre deux variables ou plus. Microsoft Excel fournit tous les outils nécessaires pour exécuter une analyse de corrélation. Vous devez juste savoir comment les utiliser.
Qu'est-ce que la corrélation ?
Avant de commencer, discutons de la définition de la corrélation. C’est une simple mesure de la façon dont les choses sont liées. Jetons un coup d’œil à deux variables qui n’ont aucune corrélation.
Le coefficient de corrélation mesure l'association entre deux variables. Les corrélations sont présentées sous forme de valeurs comprises entre -1 et 1, allant de l'absence de corrélation à la corrélation positive. En d'autres termes, il y a moins de corrélation avec un nombre plus proche de -1 et une corrélation plus élevée à mesure que vous vous rapprochez de 1. En général, quand une variable augmente, l'autre augmente. C'est la corrélation. (Notez que cela peut aussi être l’inverse ; si l’une monte et l’autre tombe, c’est une corrélation négative.)
En d’autres termes La corrélation mesure la relation linéaire de deux variables. En mesurant et en reliant la variance de chaque variable, la corrélation donne une indication de la force de la relation. Autrement dit, la corrélation répond à la question suivante : dans quelle mesure la variable A (la variable indépendante) explique-t-elle la variable B (la variable dépendante) ?
La corrélation n'égale pas la causalité ! C'est simplement une valeur pour montrer comment deux variables bougent lorsqu'elles sont comparées. Par exemple, les ventes de café ont une corrélation positive avec les retards de trafic. Maintenant, on ne peut pas dire que les achats de café causent des embouteillages… mais, en réalité, la plupart des gens achètent du café le matin en se rendant au travail.
Alors, comment calcule-t-on un coefficient de corrélation entre deux variables ? Des progiciels statistiques avancés sont disponibles, tels que SPSS. Ou, nous pourrions utiliser Excel.
La corrélation dans Excel - les bases
La corrélation est une mesure qui décrit la force et la direction d'une relation entre deux variables. Il est couramment utilisé dans les statistiques, l'économie et les sciences sociales pour les budgets, les plans d'entreprise, etc.
La méthode utilisée pour étudier le degré de corrélation entre les variables s'appelle l'analyse de corrélation. Voici quelques exemples de corrélation forte :
- Le nombre de calories que vous mangez et votre poids (corrélation positive)
- La température extérieure et vos factures de chauffage (corrélation négative)
Et voici les exemples de données qui ont une corrélation faible ou nulle :
- Le nom de votre chat et son plat préféré
- La couleur de vos yeux et votre taille
Une chose essentielle à comprendre à propos de la corrélation est qu’elle montre seulement à quel point deux variables sont étroitement liées. La corrélation, cependant, n'implique pas la causalité. Le fait que les changements dans une variable soient associés aux changements dans l’autre variable ne signifie pas qu’une variable entraîne en réalité le changement de l’autre.
Coefficient de corrélation dans Excel - interprétation de la corrélation
La mesure numérique du degré d’association entre deux variables continues est appelée coefficient de corrélation(r).
La valeur du coefficient est toujours comprise entre -1 et 1 et mesure à la fois la force et la direction de la relation linéaire entre les variables.
Force
Plus la valeur absolue du coefficient est grande, plus la relation est forte :
- Les valeurs extrêmes -1 et 1 indiquent une relation linéaire parfaite lorsque tous les points de données tombent sur une ligne. En pratique, une corrélation parfaite, positive ou négative, est rarement observée.
- Un coefficient de 0 n'indique aucune relation linéaire entre les variables. C’est ce que vous obtiendrez probablement avec deux séries de nombres aléatoires.
- Les valeurs comprises entre 0 et + 1 / -1 représentent une échelle de relations faibles, modérées et fortes. À mesure que r se rapproche de -1 ou 1, la force de la relation augmente.
Direction
Le signe de coefficient (plus ou moins) indique la direction de la relation.
- Les coefficients positifs représentent une corrélation directe et produisent une pente ascendante sur un graphique - à mesure qu'une variable augmente, l'autre augmente, et inversement.
- Les coefficients négatifs représentent une corrélation inverse et produisent une pente descendante sur un graphique - à mesure qu'une variable augmente, l'autre variable tend à diminuer.
Pour une meilleure compréhension, veuillez consulter les graphiques de corrélation suivants :
- Un coefficient de 1 signifie une relation positive parfaite - à mesure qu'une variable augmente, l'autre augmente proportionnellement.

- Un coefficient de -1 signifie une relation négative parfaite - à mesure qu'une variable augmente, l'autre diminue proportionnellement.

- Un coefficient de 0 signifie qu'il n'y a pas de relation entre deux variables - les points de données sont dispersés sur tout le graphique.

Analyse de corrélation avec Excel
Le coefficient de corrélation permet aux chercheurs de déterminer s’il existe une relation linéaire possible entre deux variables mesurées sur le même sujet (ou entité). Lorsque ces deux variables sont de nature continue (il s’agit de mesures telles que le poids, la taille, la longueur, etc.), la mesure de l’association la plus souvent utilisée est le coefficient de corrélation de Pearson.
Cette association peut être exprimée sous forme d'un nombre (le coefficient de corrélation) compris entre 1 et +1. La corrélation de population est généralement exprimée par la lettre grecque rho (r) et la statistique d'échantillon (coefficient de corrélation) est r.
La corrélation mesure dans quelle mesure une ligne droite passe par une dispersion de points lorsqu'elle est tracée sur un axe x y. Si la corrélation est positive, cela signifie que lorsqu'une variable augmente, l'autre tend à augmenter. Si la corrélation est négative, cela signifie que lorsqu'une variable augmente, l'autre tend à diminuer. Lorsqu'un coefficient de corrélation est proche de +1 (ou 1), cela signifie qu'il existe une forte corrélation, les points sont dispersés le long d'une ligne droite. Par exemple, une corrélation r = 0,7 peut être considérée comme forte. Cependant, plus un coefficient de corrélation se rapproche de 0, plus la relation est faible, lorsque le nuage (dispersion) de points n'est pas proche d'une ligne droite. Par exemple, une corrélation r = 0.1 peut être considérée comme faible.
Corrélation de Pearson
Hypothèses : Avant d'utiliser le coefficient de corrélation de Pearson comme mesure d'association, vous devez connaître ses hypothèses et ses limites. Comme mentionné précédemment, ce coefficient de corrélation mesure une relation linéaire. C'est-à-dire que la relation entre les deux variables mesure à quel point les deux mesures forment une ligne droite lorsqu'elles sont tracées sur un graphique x-y. Par conséquent, il est important que les données soient représentées graphiquement avant que la corrélation ne soit interprétée. Par exemple, il est possible que les données, lorsqu'elles sont tracées, puissent montrer une relation courbe au lieu d'une ligne droite. Dans ce cas, une corrélation de Pearson peut ne pas être la meilleure mesure de l'association. Il existe d'autres conditions dans lesquelles un coefficient de corrélation peut sembler important, mais considéré à la lumière d'un graphique, il ne constitue pas une bonne mesure de la relation. Dans les graphiques suivants, ils ont tous un coefficient de corrélation d'environ 0,95 mais la plupart ne correspondent pas à l'hypothèse d'une relation linéaire. Pour éviter une mauvaise interprétation d'une corrélation, accompagnez toujours le calcul d'un graphique.
En statistique, on mesure plusieurs types de corrélation en fonction du type de données avec lequel vous travaillez. Dans ce tutoriel, nous allons nous concentrer sur le plus courant.
La corrélation de Pearson, dont le nom complet est PPMC (Pearson Product Moment Correlation), est utilisée pour évaluer les relations linéaires entre les données lorsqu'un changement dans une variable est associé à un changement proportionnel dans l'autre variable. En termes simples, la corrélation de Pearson répond à la question suivante : les données peuvent-elles être représentées sur une ligne ?
En statistique, il s’agit du type de corrélation le plus répandu. Si vous utilisez un « coefficient de corrélation » sans autre précision, il s’agira probablement du facteur de Pearson. Voici la formule la plus couramment utilisée pour trouver le coefficient de corrélation de Pearson, également appelé « R de Pearson ».
Formule de corrélation de Pearson :

Parfois, vous pouvez rencontrer deux autres formules pour calculer le coefficient de corrélation de l'échantillon (r) et le coefficient de corrélation de la population (?).
Comment faire la corrélation de Pearson dans Excel
Le calcul manuel du coefficient de corrélation de Pearson implique pas mal de calculs. Heureusement, Microsoft Excel a rendu les choses très simples. En fonction de votre ensemble de données et de votre objectif, vous êtes libre d'utiliser l'une des techniques suivantes :
- Trouvez le coefficient de corrélation de Pearson avec la fonction COEFFICIENT.CORRELATION.
- Créez une matrice de corrélation en effectuant une analyse des données.
- Trouvez plusieurs coefficients de corrélation avec une formule.
- Tracez un graphique de corrélation pour obtenir la représentation visuelle de la relation de données.
Comment calculer le coefficient de corrélation dans Excel
Pour calculer manuellement un coefficient de corrélation, vous devez utiliser cette longue formule. Pour trouver le coefficient de corrélation dans Excel, utilisez la fonction COEFFICIENT.CORRELATION ou PEARSON et obtenez le résultat en une fraction de seconde.
La fonction Excel COEFFICIENT.CORRELATION :
La fonction COEFFICIENT.CORRELATION renvoie le coefficient de corrélation de Pearson pour deux ensembles de valeurs. Sa syntaxe est très simple et facile à utiliser :
COEFFICIENT.CORRELATION (matrice1 ; matrice2)
Où :
- Matrice1 est la première plage de valeurs.
- Matrice2 est la deuxième plage de valeurs.
Les deux tableaux doivent avoir la même longueur.
On suppose que nous ayons un ensemble de variables indépendantes (x) dans B2: B13 et de variables dépendantes (y) dans C2: C13 comme illustré dans la capture ci-dessous.

Notre formule du coefficient de corrélation va comme suit :
= COEFFICIENT.CORRELATION (B2: B13 ; C2: C13)
Ou, nous pourrions échanger les gammes et obtenir le même résultat :
= COEFFICIENT.CORRELATION(C2: C13 ; B2: B13)
Quoi qu'il en soit, la formule montre une forte corrélation négative (environ -0,97) entre la température mensuelle moyenne et le nombre d'appareils de chauffage vendus comme vous pouvez le voir dans la capture d’écran ci-dessous :
3 choses à savoir sur la fonction COEFFICIENT.CORRELATION dans Excel
Pour calculer le coefficient de corrélation dans Excel avec succès, veuillez garder à l’esprit ces 3 faits simples :
- Si une ou plusieurs cellules d'un tableau contiennent du texte, des valeurs logiques ou des blancs, ces cellules sont ignorées. les cellules avec des valeurs nulles sont calculées.
- Si les tableaux fournis ont des longueurs différentes, une erreur # N / A est renvoyée.
- Si l'un des tableaux est vide ou si l'écart type de leurs valeurs est égal à zéro, un signe # DIV / 0! erreur se produit.
Fonction Excel PEARSON
La fonction PEARSON dans Excel fait la même chose - calcule le coefficient de corrélation produit-moment de Pearson (PPMCC).
PEARSON (matrice1 ; matrice2)
Où :
- Matrice1 est une plage de valeurs indépendantes.
- Matrice2 est une plage de valeurs dépendantes.
Étant donné que PEARSON et COEFFICIENT.CORRELATION calculent tous deux le coefficient de corrélation linéaire de Pearson, leurs résultats doivent concorder, comme ils le font généralement dans les versions récentes d'Excel 2007 à Excel 2019.
Dans Excel 2003 et les versions antérieures, toutefois, la fonction PEARSON peut afficher des erreurs d’arrondi. Par conséquent, dans les versions plus anciennes, il est recommandé d’utiliser COEFFICIENT.CORRELATION plutôt que PEARSON.
Sur notre échantillon de données, les deux fonctions présentent les mêmes résultats :
= COEFFICIENT.CORRELATION (B2:B13 ; C2:C13)
= PEARSON (B2:B13 ; C2:C13)
Comment créer une matrice de corrélation dans Excel avec l’utilitaire d’analyse
Qu'est-ce qu'une matrice de corrélation ?
Une matrice de corrélation est simplement un tableau qui affiche les coefficients de corrélation pour différentes variables. La matrice décrit la corrélation entre toutes les paires de valeurs possibles dans un tableau. C'est un outil puissant pour résumer un grand ensemble de données et pour identifier et visualiser des modèles dans les données fournies.
Une matrice de corrélation est constituée de lignes et de colonnes montrant les variables. Chaque cellule d'une table contient le coefficient de corrélation. Le coefficient de corrélation le plus couramment utilisé est le coefficient de corrélation Pearson.
De plus, la matrice de corrélation est fréquemment utilisée en conjonction avec d’autres types d’analyses statistiques. Par exemple, cela peut être utile dans l'analyse de plusieurs modèles de régression linéaire. Rappelez-vous que les modèles contiennent plusieurs variables indépendantes. Dans la régression linéaire multiple, la matrice de corrélation détermine les coefficients de corrélation entre les variables indépendantes d'un modèle.
Créer la matrice de corrélation
Lorsque vous devez tester les interrelations entre plus de deux variables, il est logique de construire une matrice de corrélation, parfois appelée coefficient de corrélation multiple. La matrice de corrélation est un tableau qui montre les coefficients de corrélation entre les variables à l'intersection des lignes et des colonnes correspondantes.
La matrice de corrélation dans Excel est créée à l'aide de l'outil « Corrélation » du complément « Analysis ToolPak ». Ce complément est disponible dans toutes les versions d'Excel 2003 à Excel 2019, mais n'est pas activé par défaut. Si vous ne l'avez pas encore activé, procédez comme suit en suivant :
Dans votre Excel, cliquez sur « Fichier » puis allez dans « Options ».
Dans la boîte de dialogue « Options » Excel, sélectionnez « Compléments » dans la barre latérale gauche, assurez-vous que « Compléments Excel » est sélectionné dans la zone « Gérer », puis cliquez sur « Atteindre ».
Dans la boîte de dialogue Compléments, cochez « Analysis Toolpak », puis cliquez sur OK. Cela ajoutera les outils d'analyse de données à l'onglet « Données » de votre ruban Excel.
Avec les outils d'analyse de données ajoutés à votre ruban Excel, vous êtes prêt à exécuter une analyse de corrélation :
Maintenant dans le coin supérieur droit de l'onglet « Données » puis sur Groupe « Analyse », cliquez sur le bouton « Utilitaire d’analyse ». Ensuite dans la boîte de dialogue « Utilitaire d’analyse », sélectionnez « Analyse de corrélation » et cliquez sur OK.
Une nouvelle boite de dialogue apparaîtra, dans laquelle configurez les paramètres de cette manière :
- Cliquez dans la zone « Plage d'entrée » et sélectionnez la plage avec vos données source, y compris les en-têtes de colonne (B1: D13 dans notre cas).
- Dans la section « Groupé par », assurez-vous que la case d'option « Colonnes » est sélectionnée (étant donné que vos données source sont regroupées en colonnes).
- Cochez la case « Intitulée en première ligne » si la plage sélectionnée contient des en-têtes de colonne.
- Choisissez l'option de sortie souhaitée dans la zone « Option de sortie ». Pour que la matrice se trouve dans la même feuille, sélectionnez « Plage de sortie » et spécifiez la référence à la cellule la plus à gauche dans laquelle la matrice doit être sortie (A18 dans cet exemple).
Une fois terminé, cliquez sur le bouton OK.
Votre matrice de coefficients de corrélation est terminée et devrait ressembler à ce qui est montré dans la section suivante.
Interprétation des résultats de l'analyse de corrélation
Dans votre matrice de corrélation Excel, vous pouvez trouver les coefficients à l'intersection des lignes et des colonnes. Si les coordonnées de colonne et de ligne sont identiques, la valeur 1 est sortie.
Dans l'exemple ci-dessus, nous sommes intéressés à connaître la corrélation entre la variable dépendante (nombre d'appareils de chauffage vendus) et deux variables indépendantes (température mensuelle moyenne et coûts publicitaires). Nous ne regardons donc que les chiffres à l'intersection de ces lignes et colonnes, qui sont mis en évidence dans la capture d'écran ci-dessous :

Le coefficient négatif de -0,97 (arrondi à 2 décimales) montre une forte corrélation inverse entre la température mensuelle et les ventes d'appareils de chauffage - à mesure que la température augmente, moins d'appareils de chauffage sont vendus.
Le coefficient positif de 0,95 (arrondi à la deuxième décimale) indique un lien direct étroit entre le budget publicitaire et les ventes - plus vous dépensez d'argent en publicité, plus les ventes sont élevées.
Comment faire une analyse de corrélation multiple dans Excel avec des formules
Construire la table de corrélation avec l'outil d'analyse de données est facile. Cependant, cette matrice est statique, ce qui signifie que vous devrez exécuter une nouvelle analyse de corrélation chaque fois que les données source seront modifiées.
La bonne nouvelle est que vous pouvez facilement créer vous-même un tableau de corrélation similaire et que cette matrice sera mise à jour automatiquement à chaque changement des valeurs source. Pour le faire, utilisez cette formule générique :
COEFFICIENT.CORRELATION (DECALER (Réf ; 0 ; LIGNES ($ 1: 1) -1) ; DECALER (Réf ; 0 ; COLONNES ($ A: A) -1))
Note importante ! Pour que la formule fonctionne, vous devez verrouiller la première plage de variables en utilisant des références de cellules absolues. Dans notre cas, la première plage de variables est $ B $ 2: $ B $ 13 (veuillez noter le signe $ qui verrouille la référence), et notre formule de corrélation prend cette forme:
= COEFFICIENT.CORRELATION(DECALER($B$2:$B$13; 0; LIGNES($1:1)-1); DECALER($B$2:$B$13; 0; COLONNES($A:A)-1))
Avec la formule prête, construisons une matrice de corrélation :
- Dans la première ligne et la première colonne de la matrice, tapez les étiquettes des variables dans le même ordre qu'elles apparaissent dans votre tableau source (voir la capture d'écran ci-dessous).
- Entrez la formule ci-dessus dans la cellule la plus à gauche (F2 dans notre cas).
- Faites glisser la formule vers le bas et vers la droite pour la copier dans autant de lignes et de colonnes que nécessaire (3 lignes et 3 colonnes dans notre exemple).
En conséquence, nous avons la matrice suivante avec plusieurs coefficients de corrélation. Veuillez noter que les coefficients renvoyés par notre formule sont exactement les mêmes que ceux générés par Excel dans l'exemple précédent (les coefficients correspondants sont mis en évidence) :
La matrice que vous allez obtenir doit ressembler à ceci :

Comment fonctionne cette formule
Comme vous le savez déjà, la fonction Excel COEFFICIENT.CORRELATION renvoie le coefficient de corrélation pour deux ensembles de variables que vous spécifiez. Le principal défi consiste à fournir les plages appropriées dans les cellules correspondantes de la matrice. Pour cela, vous entrez uniquement la première plage de variables dans la formule et utilisez les fonctions suivantes pour effectuer les ajustements nécessaires :
DECALER - renvoie une plage correspondante à un nombre donné de lignes et de colonnes d'une plage spécifiée.
LIGNES et COLONNES - renvoient le nombre de lignes et de colonnes d'une plage, respectivement. Dans notre formule de corrélation, les deux sont utilisés dans un seul but : obtenir le nombre de colonnes à décaler de la plage de départ. Et ceci est réalisé en utilisant intelligemment des références absolues et relatives. Pour mieux comprendre la logique, voyons comment la formule calcule les coefficients mis en évidence dans la capture d'écran ci-dessus.
Commençons par examiner la formule de F4, qui établit une corrélation entre la température mensuelle (B2: B13) et les appareils de chauffage vendus (D2: D13):
= COEFFICIENT.CORRELATION(DECALER($B$2:$B$13; 0; LIGNES($1:3)-1); DECALER($B$2:$B$13; 0; COLONNES($A:A)-1))
Dans la première fonction DECALER ; LIGNES($ 1: 1) a été transformé en LIGNES ($ 1: 3), car la deuxième coordonnée est relative. Elle est donc modifiée en fonction de la position relative de la ligne où la formule est copiée (2 lignes vers le bas). Ainsi, LIGNES() renvoie 3, auquel nous soustrayons 1, et obtenons une plage de 2 colonnes à droite de la plage source, c'est-à-dire $D$2: $D$13 (ventes d'appareils de chauffage).
Le second DECALER ne modifie pas la plage spécifiée $B$2: $B$13 (température) car COLONNES($A: A) -1 renvoie zéro. En conséquence, notre formule longue se transforme en une simple COEFFICIENT.CORRELATION($D$2:$D$13 ; $B$2: $B$13) et retourne exactement le coefficient que nous voulons.
La formule en G4 qui calcule un coefficient de corrélation pour les coûts publicitaires (C2:C13) et les ventes (D2:D13) fonctionne de la même manière:
= COEFFICIENT.CORRELATION(DECALER($B$2:$B$13; 0; LIGNES($1:3)-1); DECALER($B$2:$B$13; 0; COLONNES($A:B)-1))
La première fonction DECALER est absolument identique à celle décrite ci-dessus, renvoyant la plage de $D$2: $D$13 (ventes d'appareils de chauffage).
Dans le deuxième DECALER, COLONNES ($A:A) -1 devient COLONNES($ A:B) -1 car nous avons copié la colonne de la formule 1 à droite. En conséquence, DECALER obtient une plage de 1 colonne à droite de la plage source, c'est-à-dire $C$2: $C$13 (coût de la publicité).
Comment tracer un graphique de corrélation dans Excel
Lorsque vous effectuez une corrélation dans Excel, le meilleur moyen d'obtenir une représentation visuelle des relations entre vos données est de tracer un diagramme de dispersion avec une courbe de tendance. Voici comment :
Sélectionnez deux colonnes avec des données numériques, y compris les en-têtes de colonne. L'ordre des colonnes est important : la variable indépendante doit figurer dans la colonne de gauche car cette colonne doit être tracée sur l'axe des x ; la variable dépendante doit être dans la colonne de droite car elle sera tracée sur l'axe des y.
Sous l'onglet « Insertion », dans le groupe « Graphiques », cliquez sur l'icône « Insérer un nuage de points (x,y) ou un graphique en bulles ». Cela insérera immédiatement un diagramme de dispersion XY dans votre feuille de calcul ensuite cliquez avec le bouton droit de la souris sur un point de données du graphique et choisissez « Ajouter une courbe de tendance… » dans le menu contextuel et choisissez le type « Linéaire » et pour afficher la valeur de R au carré cochez la case « Afficher le coefficient de détermination (R²) sur le graphique ».
Pour notre exemple de jeu de données, les graphiques de corrélation se présentent comme indiqué dans l'image ci-dessous. De plus, nous avons affiché la valeur R au carré, également appelée coefficient de détermination. Cette valeur indique dans quelle mesure la courbe de tendance correspond aux données : plus R² est proche de 1, meilleur est l'ajustement.
À partir de la valeur R² affichée sur votre diagramme de dispersion, vous pouvez facilement calculer le coefficient de corrélation :
Pour une meilleure précision, demandez à Excel d’afficher plus de chiffres dans la valeur R-carré que par défaut. Pour ce faire cliquez sur la valeur R² du graphique, sélectionnez-la à l'aide de la souris et appuyez sur Ctrl + C pour la copier.
Obtenez une racine carrée de R² en utilisant la fonction RACINE ou en élevant la valeur de R² copiée à la puissance de 0.5.
Par exemple, la valeur R² dans le deuxième graphique est 0,9174339392. Ainsi, vous pouvez trouver le coefficient de corrélation pour la publicité et les chaufferettes vendues avec l’une des formules suivantes :
= RACINE(0,9174339392)
= 0,9174339392^ 0,5
Comme vous pouvez vous en assurer, les coefficients ainsi calculés sont parfaitement en ligne avec les coefficients de corrélation trouvés dans les exemples précédents, à l'exception du signe :

Corrélation de Spearman
La corrélation de Spearman est la version non paramétrique du coefficient de corrélation de Pearson qui mesure le degré d'association entre deux variables en fonction de leurs rangs. La corrélation de Moment du produit Pearson teste la relation linéaire entre deux variables continues. Linéaire signifie une relation lorsque deux variables changent dans la même direction à un taux constant.
La corrélation de rang de Spearman évalue la relation monotone entre les valeurs classées. Dans une relation monotone, les variables ont aussi tendance à changer ensemble, mais pas nécessairement à un taux constant.
Quand faire la corrélation de Spearman
L'analyse de corrélation de Spearman doit être utilisée dans l'une des circonstances suivantes, lorsque les hypothèses sous-jacentes de la corrélation de Pearson ne sont pas satisfaites :
- Si vos données présentent une relation non linéaire ou ne sont pas distribuées normalement.
- Si au moins une variable est ordinale. Si vos valeurs peuvent être placées dans l'ordre "premier, deuxième, troisième…", vous avez affaire à des données ordinales.
- S'il y a des valeurs aberrantes significatives. Contrairement à la corrélation de Pearson, la corrélation de Spearman n'est pas sensible aux valeurs aberrantes car elle effectue des calculs sur les rangs, de sorte que la différence entre les valeurs réelles n'a pas de sens.
Par exemple, vous pouvez utiliser la corrélation de Pearson pour trouver les réponses à la questions suivante :
- Les personnes plus instruites sont-elles plus préoccupées par l'environnement ?
Coefficient de corrélation de Spearman
En statistique, le coefficient de corrélation de Spearman est représenté soit par rs, soit par la lettre grecque ? ("rho"), raison pour laquelle on l'appelle souvent rho de Spearman.
Le coefficient de corrélation de rang de Spearman mesure à la fois la force et la direction de la relation entre les rangs de données. Il peut s'agir d'une valeur comprise entre -1 et 1, et plus la valeur absolue du coefficient est proche de 1, plus la relation est forte:
- 1 est une corrélation positive parfaite
- -1 est une corrélation négative parfaite
- 0 n'est pas une corrélation
Formule de corrélation de rang de Spearman
Selon qu'il existe ou non des liens dans le classement (le même rang est attribué à deux observations ou plus), le coefficient de corrélation de Spearman peut être calculé à l'aide de l'une des formules suivantes.
S'il n'y a pas de rangs liés, une formule plus simple fera :

Où:
di est la différence entre une paire de rangs
n est le nombre d'observations
Pour traiter les rangs liés, il faut utiliser la version complète de la formule de corrélation de Spearman, qui est une version légèrement modifiée du r de Pearson :

Où :
R (x) et R (y) sont les rangs des variables x et y
R(x) barré et R(y) barré sont les rangs moyens
Comment calculer la corrélation de Spearman dans Excel avec la fonction COEFFICIENT.CORRELATION
Malheureusement, Excel ne possède pas de fonction intégrée permettant de calculer le coefficient de corrélation de rang de Spearman. Cependant, cela ne signifie pas que vous devrez vous creuser la tête avec les formules ci-dessus. En manipulant un peu Excel, nous pouvons trouver un moyen beaucoup plus simple de faire la corrélation de Spearman.
À titre d’exemple, essayons de déterminer si notre activité physique a un lien quelconque avec notre tension artérielle. Dans la colonne B, nous avons le nombre de minutes que dix hommes du même âge passent quotidiennement dans un gymnase et dans la colonne C, nous avons leur pression artérielle systolique.

Pour trouver le coefficient de corrélation Spearman dans Excel, procédez comme suit :
1- Classez vos données
Dans la mesure où la corrélation de Spearman évalue les associations entre deux variables en fonction de leur classement, vous devez classer vos données source. Cela peut être rapidement fait en utilisant la fonction Excel MOYENNE.RANG.
Pour classer la première variable (activité physique), entrez la formule ci-dessous dans D2, puis faites-la glisser jusqu'à D11 :
= MOYENNE.RANG (B2 ; $B$2: $B$11 ;0)
Pour classer la deuxième variable (pression artérielle), insérez la formule suivante dans la cellule E2 et copiez-la dans la colonne :
= MOYENNE.RANG(C2 ;$C$2:$C$11 ;0)
Pour que les formules fonctionnent correctement, veillez à verrouiller les plages avec des références de cellules absolues.
À ce stade, vos données source devraient ressembler à ceci :

2- Trouver le coefficient de corrélation de Spearman
Avec les rangs établis, nous pouvons maintenant utiliser la fonction Excel COEFFICIENT.CORRELATION pour obtenir le « rho » de Spearman :
= COEFFICIENT.CORRELATION(D2:D11 ; E2:E11)
La formule renvoie un coefficient de -0,7576 (arrondi à 4 chiffres), ce qui indique une corrélation négative assez forte et nous permet de conclure que plus une personne fait de l'exercice, plus sa pression artérielle est basse.
Le coefficient de corrélation de Pearson pour le même échantillon (-0,7445) indique une corrélation un peu plus faible, mais toujours statistiquement significative :

Corrélation vs régression linéaire dans Excel
La corrélation est une mesure simple : à quel point deux variables sont-elles liées ? Cependant, cette mesure n’a aucune valeur prédictive ou causative. Ce n’est pas parce que deux variables sont corrélées que l’une provoque des changements dans l’autre. C’est une chose cruciale à comprendre à propos de la corrélation.
Si vous souhaitez faire une déclaration sur la causalité, vous devez utiliser la régression linéaire. Vous pouvez également y accéder via l'outil d'analyse des données. (Cet article ne traitera pas en détail du fonctionnement de la régression linéaire.)
La corrélation et la régression sont les deux analyses basées sur la distribution multivariée. Une distribution multivariée est décrite comme une distribution de plusieurs variables. La corrélation est décrite comme l’analyse qui permet de connaître l’association ou l’absence de relation entre deux variables « x » et « y ». De l’autre côté, l’analyse de régression prédit la valeur de la variable dépendante en fonction de la valeur connue de la variable indépendante, en supposant que la relation mathématique moyenne existe entre deux variables ou plus.
Problèmes potentiels de corrélation dans Excel
La corrélation « Moment du produit de Pearson » révèle uniquement une relation linéaire entre les deux variables. Cela signifie que vos variables peuvent être fortement liées d'une autre manière, curviligne, et que le coefficient de corrélation est toujours égal ou proche de zéro.
La corrélation de Pearson ne permet pas de distinguer les variables dépendantes et indépendantes. Par exemple, lorsque vous utilisez la fonction COEFFICIENT.CORRELATION pour trouver le lien entre une température mensuelle moyenne et le nombre d'appareils de chauffage vendus, vous obtenez un coefficient de -0,97, ce qui indique une corrélation négative élevée. Cependant, vous pouvez changer de variable et obtenir le même résultat. On peut donc en conclure que les ventes élevées des appareils de chauffage font baisser la température, ce qui n’a évidemment aucun sens. Par conséquent, lorsque vous exécutez une analyse de corrélation dans Excel, tenez compte des données que vous fournissez.
En outre, la corrélation de Pearson est très sensible aux valeurs aberrantes. Si vous avez un ou plusieurs points de données très différents du reste des données, vous pouvez obtenir une image déformée de la relation entre les variables. Dans ce cas, il serait sage d'utiliser plutôt la corrélation de rang de Spearman.
