Exercices Circuit combinatoire simple ET séquentielle - Compteur de Johnson

Exercice 1 : Circuit combinatoire simple On souhaite construire un circuit combinatoire à trois entrées (de 1 bit chacune) et une sortie (de 1 bit) réalisant la fonction << majorité >> (notée maj sur le schéma). Le principe est que la sortie vaut 1 si une majorité d’entrées vaut 1 (c’est-à-dire deux d’entre elles ou les trois), et vaut 0 sinon.
	a b		Maj   ----->		m
	c

Question 1(échauffement) Donnez la table de vérité de la fonction maj.

Question 2 Proposez une implémentation du circuit maj à l’aide de posidertes logiques simples.

Question 3 En vous appuyant sur la table de vérité de maj (cf question 1), expliquez' comment vous pourriez utiliser ce circuit pour calculer la retenue au sein d’un additionneur (sur 1 bit) à 3 entrées.

Exercice 2 Version séquentielle du simulateur Y86

La figure ci-contre montre les entrées du circuit combinatoire << New PC >> chargé de calculer l’adresse de la prochaine instruction que le processeur devra charger (l’entrée Bch désigne la valeur <<Branch Flag >>). Le code HCL << partiel >> décrivant ce circuit est donné sous le schéma.

Question 1 Expliquez le code HCL fourni.

Question 2 Complétez ce code pour traiter les quelques cas non gérés actuel­lement. Pour chaque ligne ajoutée, expliquez précisément le choix de la valeur résultat.

Question 3 Version pipelinée du simulateur Y86

Exercice 3 :

On considère la version pipelinée du processeur Y86 à 5 étages (Fetch, Decode, Execute, Memory, Write Back) telle que vue en cours.{sidebar id=1}

On souhaite examiner le fonctionnement du processeur lors de l’exécu­tion de la séquence d’instructions ci-contre.

New PC PC

PC = [code == Jxx && Bch : valC ; ...1 : valP ;]

irmovl $1, %eax mrmovl variable, %edx addl %eax, %edx rmmovl %edx, variable

Question 1 En supposant une version naïve du processeur se limitant à l’insertion automatique de bulles pour conserver une exécution correcte, dessinez un chronogramme montrant la progression des instructions à l’intérieur du pipeline pour chaque cycle.

Question 2 En supposant maintenant une version du processeur capable de propager des valeurs des étages E, M ou WB vers l’étage E, redessinez le chronogramme. Y a-t-il encore apparition de bulles ? Expliquez.

Question 3 Cela change-t-il quelque chose d’inverser l’ordre des deux premières instructions dans le programme d’origine? Expliquez.

'NB : On ne demande pas de dessiner l’additionneur.{sidebar id=6}

Exercice 4 Compteur de Johnson

Le compteur de Johnson ci-dessous est composé de quatre bascules D (rappel: Q' i = Qi).

On suppose qu’à l’initialisation on a l’état Q0 = Q1 = Q2 = Q3 = 0.

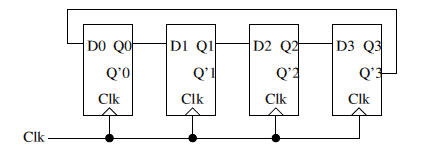
Question 1 Dresser une table des états Qi en fonction du temps (une ligne par période d’horloge). Combien de situations différentes peuvent survenir (noté N)?

Question 2 On souhaite à partir de ce circuit construire un circuit possédant N sorties étant mises à 1 tour à tour de manière cyclique. Écrivez les expressions de s1 ... sN en fonction de Q0, Q^' ₀, ... Q3, Q^'₃.

Question 3 On rappelle qu’une bascule D peut être implémenté avec 6 portes simples. Combien de portes nécessite le circuit établi à la Q2? De manière générale, combien de portes sont nécessaires (en fonction du N voulu)?

Question 4 Proposer une autre solution utilisant huit bascules D et supposant un état initial approprié. Com­bien de portes sont nécessaires? De manière générale, combien de portes sont nécessaires?

Question 5 (difficile, complémentaire) Proposer une autre solution utilisant trois bascules D et quelques circuits supplémentaires. Estimez un ordre de grandeur du nombre de portes nécessaire de manière générale.

www.eliby.com