Excel normal distribution curve template
Excel normal distribution curve template
This article provides details of Excel normal distribution curve template that you can download now.
Normal distribution graph in excel is used to represent the normal distribution phenomenon of a given data, this graph is made after calculating the mean and standard deviation for the data and then calculating the normal deviation over it, from excel 2013 versions it has been easy to plot the normal distribution graph as it has inbuilt function to calculate the normal distribution and standard deviation, the graph is very similar to the bell curve.
Microsoft Excel software under a Windows environment is required to use this template
These Excel normal distribution curve templates work on all versions of Excel since 2007.
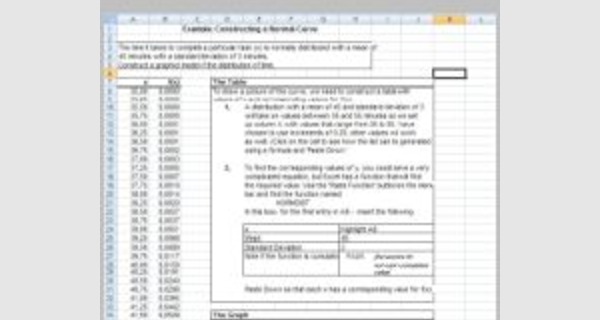
Examples of a ready-to-use spreadsheet: Download this table in Excel (.xls) format, and complete it with your specific information.
To be able to use these models correctly, you must first activate the macros at startup.
The file to download presents tow Excel templates of normal distribution curve
- simple example of Constructing a Normal Curve
- Graphing a Normal Distribution in Excel
In addition to graphing the Normal distribution curve, the normal distribution spreadsheet includes examples of the following:
- Generating a random number from a Normal distribution.
- Calculating cumulative probabilities.
- Shading a portion of the distribution (see below).
The graph shown in the screen-shot above is particularly useful for showing the relationship between the probability density function and the cumulative probability. Both the label and the shaded region change after you move the slider.
What is a normal distribution curve
In statistics, the theoretical curve that shows how often an experiment will produce a particular result.The curve is symmetrical and bell shaped, showing that trials will usually give a result near the average,but will occasionally deviate by large amounts. The width of the “bell” indicates how much confidence onecan have in the result of an experiment ,the narrower the bell, the higher the confidence. This curve is also called the Gaussian curve, after the nineteenth-century German mathematician Karl Friedrich Gauss.
Note : The normal distribution curve is often used in connection with tests in schools. Test designers often find that their results match a normal distribution curve, in which a large number of test takersdo moderately well (the middle of the bell); some do worse than average, and some do better (the sloping sides of the bell); and a very small number get very high or very low scores (the rim of thebell).
To speak specifically of any normal distribution, two quantities have to be specified: the mean , where the peak of the density occurs, and the standard deviation , which indicates the spread or girth of the bell curve. (The greek symbol is pronounced mu and the greek symbol is pronounced sig-ma.)
Different values of and yield different normal density curves and hence different normal distributions
Standard Deviation
Written by Robert Niles
I'll be honest. Standard deviation is a more difficult concept than the others we've covered. And unless you are writing for a specialized, professional audience, you'll probably never use the words "standard deviation" in a story. But that doesn't mean you should ignore this concept.
The standard deviation is kind of the "mean of the mean," and often can help you find the story behind the data. To understand this concept, it can help to learn about what statisticians call "normal distribution" of data.
A normal distribution of data means that most of the examples in a set of data are close to the "average," while relatively few examples tend to one extreme or the other.
Let's say you are writing a story about nutrition. You need to look at people's typical daily calorie consumption. Like most data, the numbers for people's typical consumption probably will turn out to be normally distributed. That is, for most people, their consumption will be close to the mean, while fewer people eat a lot more or a lot less than the mean.
When you think about it, that's just common sense. Not that many people are getting by on a single serving of kelp and rice. Or on eight meals of steak and milkshakes. Most people lie somewhere in between.
If you looked at normally distributed data on a graph, it would look something like this:
The x-axis (the horizontal one) is the value in question... calories consumed, dollars earned or crimes committed, for example. And the y-axis (the vertical one) is the number of datapoints for each value on the x-axis... in other words, the number of people who eat x calories, the number of households that earn x dollars, or the number of cities with x crimes committed.
Now, not all sets of data will have graphs that look this perfect. Some will have relatively flat curves, others will be pretty steep. Sometimes the mean will lean a little bit to one side or the other. But all normally distributed data will have something like this same "bell curve" shape.
The standard deviation is a statistic that tells you how tightly all the various examples are clustered around the mean in a set of data. When the examples are pretty tightly bunched together and the bell-shaped curve is steep, the standard deviation is small. When the examples are spread apart and the bell curve is relatively flat, that tells you you have a relatively large standard deviation.
Computing the value of a standard deviation is complicated. But let me show you graphically what a standard deviation represents...
One standard deviation away from the mean in either direction on the horizontal axis (the two shaded areas closest to the center axis on the above graph) accounts for somewhere around 68 percent of the people in this group. Two standard deviations away from the mean (the four areas closest to the center areas) account for roughly 95 percent of the people. And three standard deviations (all the shaded areas) account for about 99 percent of the people.
If this curve were flatter and more spread out, the standard deviation would have to be larger in order to account for those 68 percent or so of the people. So that's why the standard deviation can tell you how spread out the examples in a set are from the mean.
Why is this useful? Here's an example: If you are comparing test scores for different schools, the standard deviation will tell you how diverse the test scores are for each school.
Let's say Springfield Elementary has a higher mean test score than Shelbyville Elementary. Your first reaction might be to say that the kids at Springfield are smarter.
But a bigger standard deviation for one school tells you that there are relatively more kids at that school scoring toward one extreme or the other. By asking a few follow-up questions you might find that, say, Springfield's mean was skewed up because the school district sends all of the gifted education kids to Springfield. Or that Shelbyville's scores were dragged down because students who recently have been "mainstreamed" from special education classes have all been sent to Shelbyville.
In this way, looking at the standard deviation can help point you in the right direction when asking why information is the way it is.
The standard deviation can also help you evaluate the worth of all those so-called "studies" that seem to be released to the press everyday. A large standard deviation in a study that claims to show a relationship between eating Twinkies and shooting politicians, for example, might tip you off that the study's claims aren't all that trustworthy.
Of course, you'll want to seek the advice of a trained statistician whenever you try to evaluate the worth of any scientific research. But if you know at least a little about standard deviation going in, that will make your talk with him or her much more productive.
When a teacher gives an exam in class, how does he or she decide if the test scores were good or bad? This lesson focuses on classroom assessment, including specifically how to analyze the variability of scores within a given group of students. We'll discuss both standard deviation (how much the scores vary from each other) and how to interpret bell curves (a graphical representation of the distribution of scores).
Variance Of Scores In A Classroom
Imagine you're a teacher and you give your students a test over their understanding of the United States Revolutionary War. Once you grade the test, how do you know what the scores mean in terms of how well the students did? Another lesson talks about how you can quickly summarize the pattern of scores, or the average, using the concepts of mean, median, or mode. However, these concepts relate to summarizing how high or low the scores were in general. In addition to a quick average summary, you might also be interested in how much variability there was in the students. In other words, did all of the students get similar scores to each other? Or did some students do really well while other students in the same class did really badly?
The purpose of this lesson is to talk about how you can learn about the variability of scores in a classroom environment and why that might matter. We're going to cover two important concepts, which are standard deviation of scores and how to construct and interpret a bell curve based on student scores.
Standard Deviation
Let's start by using an example. Imagine you teach a class with 20 students, and they take a test with 20 multiple choice questions about the Revolutionary War. Imagine that the grades you get back from scoring their tests look like this:
| Student #1: 20 | Student #11: 10 |
| Student #2: 17 | Student #12: 10 |
| Student #3: 16 | Student #13: 10 |
| Student #4: 14 | Student #14: 8 |
| Student #5: 14 | Student #15: 8 |
| Student #6: 12 | Student #16: 8 |
| Student #7: 12 | Student #17: 6 |
| Student #8: 12 | Student #18: 6 |
| Student #9: 10 | Student #19: 4 |
| Student #10: 10 | Student #20: 3 |
Now you want to know the basic variability within the classroom. So, did the students' scores kind of clump up all together, meaning the students all showed about the same amount of knowledge? Or did the scores vary widely from each other, meaning some students did great whereas other students failed the test?
The answer to this question can come very precisely by calculating a standard deviation. A standard deviation is a number that indicates how much a group of scores vary from one another on average. Another way to say this is that the standard deviation tells you the standard, or typical, amount that scores in a group deviate, or change, within that group.
So let's look at our example from the Revolutionary War test. It looks like the scores have a pretty big range; the top score was 20, while the bottom score was only 3. But the standard deviation will give you an exact number telling you how much they really do vary within the group.
Calculating Standard Deviation
To calculate the standard deviation, it's a little complicated. First, you need to know the mean, or average, score. This equation is covered in another lesson, so we'll skip that equation for now. Just believe me that the mean score out of this group is 10.5, which is right in the middle of the pack.
The next step is that you take each score and subtract the mean from it to get a difference. So if you look at the screen, you can see that 10.5 has been subtracted from each score. For example, the top score was 20, and we subtract 10.5 from that to get a difference of 9.5. For the bottom half of the students, you end up with a negative result. For example, 3 - 10.5 equals negative 7.5. For standard deviation, it doesn't matter if the difference is positive or negative, so you can just ignore the negative sign and keep the actual number of 7.5. Do that for all of the scores in the group.
Now you just take all of those difference scores, add them up, and divide by the number of scores you had. The number you get will be the average amount the scores were different from the mean of 10.5. Here, when we add up all the difference scores, we get a total of 66. Now, we divide 66 by 20 (the number of students), and we get a final score of 3.3. The standard deviation of scores is 3.3, meaning that the average amount scores vary from the middle is between 3 and 4 points on the test.
Why It Matters
Now that we have our standard deviation of 3.3, what the heck does that mean? Well, it just gives us an idea of how much the scores on the test clumped together. To understand this better, look at the two distributions of scores on the screen. The one on the left shows scores that are all very similar to each other. So, because the scores are all close together, the standard deviation is going to be very small. But, the one on the right shows scores that are all pretty different from each other (lots of high scores on the test, but also lots of failing grades on the test). For this distribution, we'd have a high number for our standard deviation.
So why do we care about standard deviation at all? Well, a teacher would want to know this information because it might change how he or she teaches the material or how he or she constructs the test. Let's say that there's a small standard deviation because all of the scores clustered together right around the top, meaning almost all of the students got an A on the test. That would mean that the students all demonstrated mastery of the material. Or, it could mean that the test was just too easy! You could also get a small standard deviation if all of the scores clumped together on the other end, meaning most of the students failed the test. Again, this could be because the teacher did a bad job explaining the material or it could mean that the test is too difficult.
Most teachers want to get a relatively large standard deviation because it means that the scores on the test varied from each other. This would indicate that a few students did really well, a few students failed, and a lot of the students were somewhere in the middle. When you have a large standard deviation, it usually means that the students got all the different possible grades (like As, Bs, Cs, Ds, and Fs). So, the teacher can know that he or she taught the material correctly (because at least some of the students got an A) and the test was neither too difficult nor too easy.
So, we can get a good idea of the pattern of variability using this idea of standard deviation. However, there's one more way you can look at the pattern of scores. That's our last topic for this lesson, and it's the idea of bell curves.
Bell Curves
To construct a bell curve, you plot the test scores in a graph. The x-axis is for the score received and the y-axis is for the number of students who got that score. So still using our same example of 20 students who took a test with 20 questions, you can see here the pattern that shows up on the graph. There's a big bump in the middle, showing the five students who got the middle score of 10. Then, the graph tapers off on each side, indicating that fewer students got very high or very low scores.
Remember that before, we said that most teachers will want their students' scores to look kind of like what we see here. We had a lot of scores that fell in the middle (indicated by the big bump), which might be like a letter grade of a C. We had a few students who did really well (which might be like the grade of A) and a few students who did badly (in other words, they got an F). When you have a bell curve that looks like this one, with a bump in the middle and little ends on each side, it's called a normal distribution. A normal distribution has this bell shape and is called normal because it's the most common distribution that most teachers would see in a classroom.
Now, imagine that most of the students got an A on the test. What would that bell curve look like? It would look something like this one. You can see here that the bump falls along the right side of the graph (where the higher scores are), with it tapering off only on the left side, showing that most students got high scores and only a few got low scores. The exact opposite would be true if most students got an F, which would look like this graph. When a bell curve is not normal and is instead weighted heavily on either side like this, it's called a skewed distribution. Skewed distributions are both less common in classrooms and usually less desirable.
