Examen en électricité bâtiment
Les parties A et B sont totalement indépendantes
A. Étude d’une installation électrique domestique
A.1 Rappel de cours
Un dipôle linéaire soumis à une tension sinusoïdale u t U 2 cos t est traversé par un courant d’intensité instantanée i t I 2 cos t .
A.1.1. Que représentent précisément la valeurUainsi que et ?
A.1.2. Préciser l’expression de la puissance instantanéepdissipée dans le dipôle. Quelle est la conventionutilisée ?
A.1.3. Établir l’expression de la puissance moyennePdissipée dans le dipôle en fonction deI,Uet .
A.1.4. Préciser l’expression dePdans les cas particuliers suivants : un résistor de résistanceR, une bobined’auto-inductance L ou un condensateur de capacité C.
A.1.5 Le kilowattheure (kWh) est l'énergie consommée par un appareil d'une puissance égale à un kilowattfonctionnant pendant une heure. Quelle est sa valeur en J ?
A.2 Étude de l’installation
Une installation électrique est alimentée par un opérateur sous une tension efficace U 230 V et de
fréquence f 50 Hz . Un disjoncteur différentiel a un pouvoir de coupure si l’intensité efficace dépasse
I 2000 A avec un facteur de puissance cos 0, 7 .
A.2.1 Quelle est la valeur de la puissance maximalePmaxqui peut être dissipée dans la maison lors desutilisations domestiques électriques ?
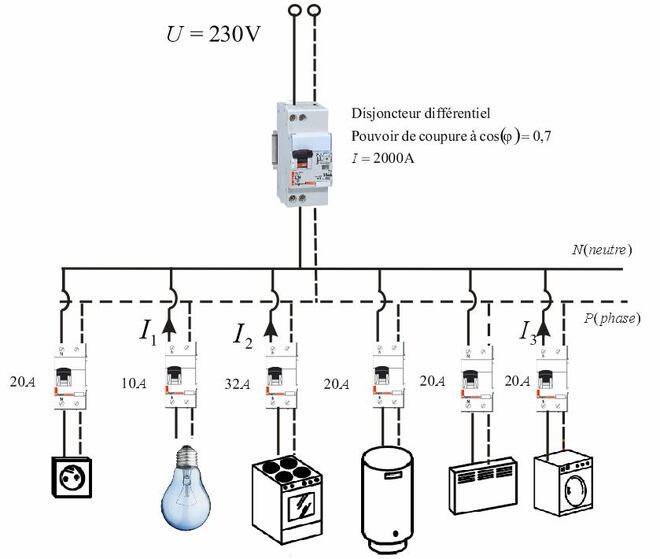
Le montage filaire simplifié de l’installation domestique est représenté sur la figure 1.
(1) (2) (3)
Figure 1 : Montage filaire simplifié de l’installation électrique
Un disjoncteur est un dispositif susceptible de couper le courant si l’intensité efficace dépasse un seuil : 10 A, 20 A ou 30 A suivant les besoins.
ü L’ensemble des prises est relié à un disjoncteur 20 A maximum,
ü L’ensemble des éclairages est relié à un disjoncteur 10 A maximum,
ü L’appareil de cuisson est relié à un disjoncteur 32 A maximum,
ü Le chauffe-eau, les convecteurs électriques et le dispositif de lavage sont reliés à un disjoncteur 20 A maximum.
Les notations des grandeurs électriques associées à l’étude de cette partie sont présentées dans le tableau 1.
| Dispositif | Éclairage | Cuisson | Lave-linge seul | Lave-linge + lave- | ||
| (foyers + four) | vaisselle en parallèle | |||||
| I3p(principal) | ||||||
| Intensité efficace | I1 | I2 | I3 | I3lp(lave-linge) | ||
| I3vp(lave-vaisselle) | ||||||
| Puissance maximale de l’appareil |
P1 | P2f | (foyers) | P3l | P3l(lave-linge) | |
| P2F(four) | P3v(lave-vaisselle) | |||||
| Facteur de puissance | cos 3l | cos 3l (lave-linge) | ||||
| cos 3v (lave-vaisselle) | ||||||
Tableau 1 : Notation des grandeurs électriques associées à l’étude de la partie A.2.
Les questions A.2.2. à A.2.5. sont consacrées à l’étude électrique des branchements du dispositif d’éclairage (1), du dispositif de cuisson (2) et du dispositif de lavage (3). Dans ce dernier cas, le lave-linge est d’abord utilisé seul puis branché en parallèle avec un lave-vaisselle.
| A.2.2. | L’éclairage de l’ensemble de la maison est constitué de 3 ampoules de 100 W et une ampoule de W, fonctionnant sous 230 V. Chaque ampoule est assimilée à un résistor de résistance R. |
| A.2.3 | L’appareil de cuisson est constitué de 4 foyers électriques d’une puissance maximale totale P2 f= 2000 W et d’un four électrique de puissance maximale P2F = 2500 W. L’ensemble se comporte comme un résistor. |
| Quelle est la valeur de l’intensité efficace maximale I2 du courant à la sortie du disjoncteur (2) ? | |
|
A.2.4 | Le lave-linge admet une puissance maximale P3l2250 W et un facteur de puissance cos 3l 0,8 . |
Le lave-linge est modélisé par l’association en série d’un résistor de résistance R et d’une bobine d’auto-inductance L.
Sur la notice commerciale de la machine, le constructeur affirme qu’un lavage de 5 kg à 60°C consomme 0,4 kWh. La durée d’un lavage est de 75 min. L’essorage n’est pas pris en compte dans l’étude.
| Données : | V=5 L | |
| Volume d’eau utilisé pour un lavage | ||
| Température initiale avant lavage | T0= 15°C | |
| Température finale après lavage | Tf= 60°C | |
| Capacité thermique massique de l’eau | c = 4180 | J. kg-1.K-1 |
| Masse volumique de l’eau | 1000 | kg.m 3 |
Dans cette partie le lave-linge est utilisé seul dans le dispositif de lavage.
Quelle fraction de l’énergie totale l’énergie consacrée au chauffage représente-t-elle ?
g) Déduire la puissance moyenne consommée lors du chauffage de l’eau.
A.2.5 En raison de problèmes d’arrivée d’eau, le propriétaire décide de brancher en parallèle sur une prisemultiple, le lave-linge et le lave-vaisselle. Le lave-vaisselle admet une puissance maximale P3v 1600 W et un facteur de puissance cos 3v 0, 7 .
Dans cette partie, le lave-linge et le lave-vaisselle sont branchés en parallèle.
| a) | Déterminer les expressions littérales des intensités efficaces maximales I3lp et I3vpdes courants qui alimentent le lave-linge et le lave-vaisselle respectivement. Effectuer les applications numériques. |
| b) | Exprimer la nouvelle intensité efficace maximale I3pen fonction de I3lp, I3vp,3l et 3v . Effectuer l’application numérique et commenter le résultat. |
A.3. Étude de la protection d’une installation :
La carcasse métallique d’un appareil d’utilisation domestique comporte une « phase » à 230 V et un « neutre » à 0 V destinés au circuit d’alimentation. La carcasse est également reliée par un fil à la « terre » afin de protéger l’utilisateur. En cas de défaut d’isolement de l’appareil, l’utilisateur au contact de la carcasse est soumis au potentiel du réseau ; sa protection n’est pas assurée. L’absence de « terre » sur l’appareil d’utilisation ne permet pas l’écoulement du courant de défaut : seul un disjoncteur différentiel de 30 mA permettra à la personne d’éviter l’électrocution.
Si une installation monophasée présente un défaut d’isolement, le courant d’intensité efficace I qui entre dans la machine est différent du courant qui en ressort, d’intensité efficace I IF . Le courant de fuite d’intensité efficace IF passe à la terre via la personne dont la résistance électrique globale est notée R (figure 2). Le disjoncteur coupe le courant si l’intensité efficace atteint la valeur seuil IFseuil30 mA , valeur pour laquelle il y a risque detétanisation des muscles.
A.3.1. Quelle doit être la valeur maximale de la résistanceR0pour qu’il y ait coupure de courant ?
figure 2 : Courant de fuite en l’absence de« terre » sur l’appareil.
A.3.2. On peut modéliser le corps humain selon le schémaélectrique représenté sur la figure 3.
Données : R1 460 , R2 80 , R3 125 , R4 15 , R5840 .
les deux mains tiennent les deux pôles d’une prise 230 V et les chaussures sont isolantes ; une main tient une phase 230 V et les pieds nus par terre ;
les deux mains tiennent les rails d’un train de modélisme (16 V)
figure 3 : Modèle électriquedu corps humain
Afin de protéger une installation, on ajoute un fil de terre (jaune et vert) relié à une tige très conductrice de forme cylindrique plantée sur une longueur L dans le sol, de rayon rTet terminée par une extrémité hémisphérique. Le dispositif de la tige dans la terre est représenté sur la figure 4.
A.3.3
figure 4 : Aspects géométriques de l’implan-tation d’une tige dans le sol
…
A.3.4 Le code de l’électricité demande que la résistance de mise à la terre soit inférieure à25. La solutionconsiste à placer plusieurs tiges en parallèle selon le schéma représenté sur la figure 5.a. À cette disposition est associé un schéma électrique équivalent représenté sur la figure 5.b . R1 est la résistance d’un câble de diamètre D 8 mm et de conductivité 6.107 S.m 1 . R2 est la résistance du sol. On prendra R2 = 30 Ω. La distance entre deux tiges voisines est d 5 m .
| figure 5.a : Dispositif de mise à la terre | figure 5.b : Schéma électrique équivalent de la mise à la terre |
Déterminer la relation de récurrence entre Rn et Rn1 .
c) Lorsque n tend vers l’infini, la résistance entre A et B tend vers une limite finie. Déterminer l’expression de cette limite en fonction de R1 et R2 .
Étude physique appliquée aux phénomènes biologiques : anévrisme et sténose
B.1 : Rappels de cours : loi de Poiseuille et résistance hydraulique - Application
B.1.1. Un tronçon cylindrique de rayonRet de longueurLest traversé par un fluide de viscosité et de masse volumique µ. Les phénomènes de pesanteur sont négligés dans l’étude.
Rappeler la loi de Poiseuille reliant le débit volumique Q à la différence de pression aux extrémités du cylindre.
Préciser les conditions de validité de cette loi.
B.1.2. Le termeQreprésentant le débit volumique à travers la section droiteS, on définitRHy,résistance
hydrodynamique, par la relation P0– PL= RHyQ, où P0 et PL sont, respectivement, les pressions à l’entrée et à la sortie du tronçon cylindrique.
Exprimer la résistance hydraulique RHy en fonction de L,R et .
B.1.3. Rappeler l’expression du nombre de ReynoldsRe. Rappeler le domaine dans lequel se situe la valeur de
Repour un écoulement de Poiseuille. Déduire une condition portant sur le rayon R et effectuerl’application numérique.
| Données : | vmoy= 0,1 m/s | |
|
Vitesse moyenne | ||
| Viscosité dynamique | = 10-3 | Pl |
| Masse volumique | µ = 103 | kg/m3 |
B.1.4. Un tronçon est, à présent, constitué de trois portions cylindriques, de même axe, associées en série, derayons r1 , r2 et r3 et de résistances hydrodynamiques respectives RHy1 , RHy2 et RHy3 (figure 6). La première
portion est comprise entre x0 0 et x1L1 , la deuxième portion est comprise entre x1L1 et x2L1L2 et la troisième portion est comprise entre x2L1L2 et x3l .PA , P1 , P2 et PB sont les pressions en x0 0 , x1L1 , x2 L1 L2et x3 l respectivement . Les pertes de charges au niveau des raccordements sont négligées.
…
| et RHy3 |
On pose Q QA . Montrer que l’on peut écrire PAPBRHyQ où RHy est la résistance hydrodynamique de l'ensemble du tronçon. Exprimer RHy en fonction de RHy1 , RHy2 et RHy3 . Expliciter brièvement une analogie avec un problème d’électrocinétique et préciser l’équivalence entre grandeurs physiques décrivant l’écoulement d’un fluide ou celui de porteurs de charges.
B.1.5. Déduire l’expression deP1P2en fonction de RHy1, RHy2, RHy3et PAPB.
B.2 : Étude d’un anévrisme
B.2.1. Un vaisseau sain est modélisé par un tronçon cylindrique horizontal de longueurAB = let de rayon constantr0parcouru par le sang de viscosité . Dans toute la suite, la perte de charge P PA PBest supposéeconstante, le générateur cardiaque fournit la même énergie.
Préciser l’expression de la résistance hydraulique RHy du vaisseau sain.
Établir l’expression du débit volumique sanguin Q en fonction de , l, r0 et P.
B.2.2. Le tiers central d’un tronçon de vaisseau de longueurlest le siège d’un anévrisme. Dans cette portioncentrale, le rayon moyen R0 est plus grand que le rayon moyen r0 du reste du tronçon.
Le vaisseau est partagé en trois portions de même longueur l/3 et de résistances hydrauliques respectivement
notées :
RHy1, RHy2 . La figure 7 représente la coupe diamétrale du vaisseau atteint d’anévrisme.
| P1a | P2a | ||
| r | R0> r0 | ||
| 0 | B | ||
| x = 0 | x=l /3 | x = 2 l /3 | x = l |
| RHy1 | RHy2 | RHy3 |
Figure 7 : Coupe diamétrale d’un anévrisme
Préciser les expressions des résistances hydrauliques RHy1 , RHy2 et RHy3 en fonction de la résistance hydraulique RHy du vaisseau sain et des rayons R0 et r0 .
Qaest le nouveau débit volumique sanguin dans le vaisseau atteint d’anévrisme. Préciser l’expression de Qaen fonction du débit volumique sanguin Q dans le vaisseau sain, et des rayons R0 et r0 . Comparer Qa à Q .
P1aet P2asont les nouvelles pressions, respectivement, en x = l/3 et x = 2l/3, dans le vaisseau atteintd’anévrisme. Exprimer P1a– P2a en fonction de la perte de charge P et des rayons R0 et r0 .
Comparer P1a– P2a à P/3 et évoquer un effet possible de l’anévrisme sur la personne à partir de ce résultat.
B.3 : Étude d’une sténose - Pontage
B.3.1. Le tiers central d’un tronçon d’artère de longueurlest le siège d’une sténose. Dans cette portion centrale, lerayon intermédiaire R0 est plus petit que le rayon r0 de l’artère non altérée. Le tronçon d’artère de longueur l est partagé en trois portions de même longueur l/3. La figure 8 représente la coupe diamétrale du vaisseau atteint d’une sténose.
| r | R0 | < r0 | r0 | |
| x = 0 | x=l /3 | x = 2l /3 | x = l |
Figure 8 : Coupe diamétrale d’une sténose
Déduire la nouvelle résistance hydraulique RHs de l’artère sténosée. Exprimer le résultat sous la forme
RHs = αRHy, où RHyest la résistance hydraulique de l’artère saine etα un coefficient de proportionnalité.
Expliciter α en fonction de R0 et r0 .
Qsest le nouveau débit volumique sanguin dans l’artère atteinte de sténose. Préciser l’expression de Qsenfonction de Q et des rayons R0 et r0 puis en fonction de Q et . Comparer Qs à Q. Quelle conséquence physiologique est déduite de ce résultat ?
B.3.2. Un pontage est réalisé afin de réparer une artère sténosée. Le pontage consiste à contourner l’obstacle à l’aided’une tubulure mise en parallèle sur la totalité du tronçon. RHp est la résistance hydraulique du pontage de longueur l. La figure 9 représente la coupe diamétrale du pontage.
| x = 0 | x=l /3 | x = 2l /3 | x = l |
Figure 9 : Coupe diamétrale du pontage
Préciser le schéma électrique équivalent en explicitant brièvement le choix.
Établir l’expression de la résistance hydraulique RHe équivalente de l’artère pontée en fonction de RHy, α et
RHp.
B.3.3. Quelle doit être la valeur deRHpafin de rétablir le débit volumique sanguin à sa valeur en l’absence desténose ? Exprimer, dans ce cas, RHp en fonction de RHy et .
B.3.4. Déterminer l’expression du rayonrpde la tubulure de pontage permettant de rétablir le débit volumiquesanguin à sa valeur en l’absence de sténose, en fonction de R0 et r0 .
