Tuto Python & Scikit-learn : SVM classification et régression

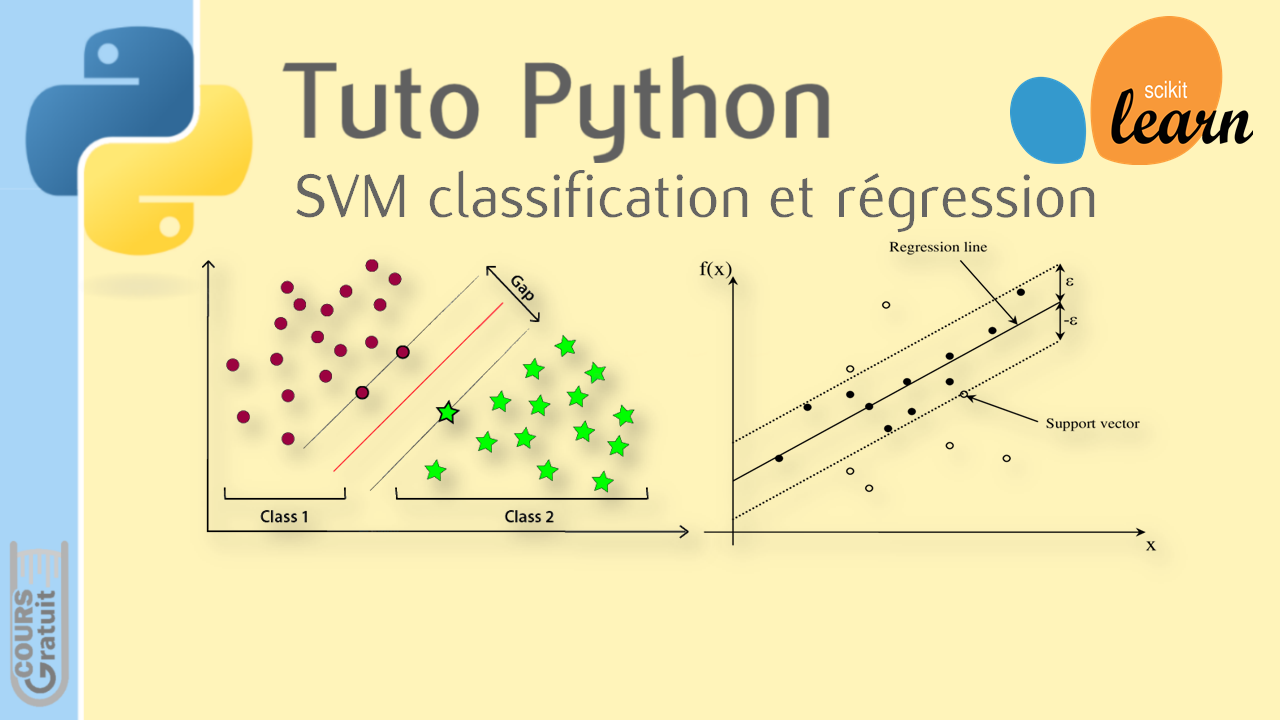
Table des matières

Introduction

1. Principede fonctionnement
2. Module Scikit-learn

2.1. SVM classification

2.2. SVM régression

3. Cas d’utilisation
4. Avantages et limites

4.1. Avantages

4.2. Limites

Conclusion

Introduction

Les machines à vecteurs de support (ou Support Vector Machine, SVM) sont une famille d’algorithmes d’apprentissage automatique de type supervisé et qui peuvent être utilisées pour des problèmes de discrimination (à quelle classe appartient un échantillon), de régression et de détection d’anomalies.

Lors de ce tutoriel nous nous intéresserons aux différents SVM de classification ainsi que de régression mise en place par la bibliothèque d’apprentissage automatique Scikit-learn de Python.

1. Principe de fonctionnement

Les SVM sont une généralisation des classifieurs linéaires (algorithmes de classement statistique)  dont le principe est de séparer les données en classe à l’aide d’une frontière, de telle façon que la distance entre les différents groupes de données et la frontière séparatrice soit maximale. Cette distance est appelée marge. Et les données les plus proches de la frontière sont appelées vecteurs de support.

Dans le schéma suivant, la frontière est la droite en rouge, les vecteurs de support sont les éléments les plus proches de la frontière entourés en vert. Finalement, la marge est la distance entre la droite en rouge et les deux droites en noire et en jaune.

2. Module Scikit-learn

2.1. SVM classification

Pour la classification, la bibliothèque scikit-learn de Python met en place trois classes : SVC, NuSVC et LinearSVC.

Afin de démontrer le fonctionnement de ces trois algorithmes (SVC, NuSVC et LinearSVC) nous allons procéder à travers l’exploitation de l’exemple de dataset « iris » et qui concerne les trois espèces de l’iris représentées comme suivant : 0 pour setosa, 1 pour versicolor et 2 pour virginica.

Tout d’abord, nous allons importer le module pandas qui nous permettra de lire le fichier csv, on importe aussi train_test_split qui nous permettra de fractionner le dataset en données de training et de test.

Ensuite, on charge le fichier CSV comprenant les données. Et on définit une variable x qui va contenir les données de caractéristique et une autre variable y pour les valeurs cibles qui sont les étiquettes de classe pour les échantillons d’entrainement.

A l’aide de la fonction head(), on affiche les cinq premières lignes de la dataset pour avoir une idée sur celle-ci.

• Code :

import pandas as pd
from sklearn.model_selection import train_test_split
#traitement du fichier csv
df = pd.read_csv( 'C:/Users/LENOVO/Desktop/coursGratuit/iris.csv')
a = df.loc[:, "petal_length"]
b = df.loc[:, "petal_width"]
x = list(zip(a, b))
y = df.loc[:, "species"]
df.head()


• Résultat de l’exécution :

2.1.1. SVC

Le SVC est un modèle de classification dont l’implémentation est basée sur libsvm.

Dans le code suivant on a tout d’abord importé la classe SVC puis on a fractionné notre dataset à l’aide de train_test_split qu’on a précédemment importé.

Puis nous avons créé une instance model_SVC de l’objet SVC. On entraine celle-ci à l’aide de la méthode fit() qu’on lui passe en paramètres x_train et y_train.

L’objet SVC peut prendre plusieurs paramètres optionnels. Dans ce qui suit, on n’utilise que les trois paramètres optionnels suivants :

- Kernel : spécifie le type de noyau à utiliser dans l’algorithme, et qui peut être soit « linear », « poly », « rbf », « sigmoid » ou « precomputed », par défaut il prend la valeur « rbf ».

- Gamma : correspond au coefficient de noyau pour les noyaux « rbf », « poly », et « sigmoid ». Prend comme valeur soit « scale », « auto » ou un nombre à virgule.

- shrinking : désigne une valeur booléenne, True si on veut utiliser l’heuristique rétrécissante, False sinon.

En faisant appel à la méthode score() on calcule la précision de ce modèle.

Puis finalement, on fait entrer la longueur et la largeur d’un iris et on demande au SVC de prédire son espèce en utilisant la méthode de predict().

• Code :

from sklearn.svm import SVC
#fractionner dataset (train-test)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.20)
#instanciation
model_SVC = SVC( kernel = 'linear', gamma = 'scale', shrinking = False,)
#training
model_SVC.fit( x_train, y_train)
#calcule de précision
print( model_SVC.score( x_test, y_test))
#Prédiction
longueur = 2.5
largeur = 0.75
prediction = model_SVC.predict( [[longueur, largeur]])
#affichage des résultats
resultat = "Résultat : "
if prediction[0] == 0:
resultat = resultat + "setosa"
if prediction[0] == 1:
resultat = resultat + "versicolor"
if prediction[0] == 2:
resultat = resultat + "virginica"
print( resultat)


• Résultat de l’exécution :

Attributs

Le tableau suivant regroupe les attributs pouvant être utilisé par la classe sklearn.svm.SVC :

On applique ces attributs au modèle précédent :

• Code :

model_SVC.fit_status_
model_SVC.coef_
model_SVC.support_
model_SVC.n_support_


• Résultat de l’exécution :

• Code :

model_SVC.support_vectors_

• Résultat de l’exécution :

• Code :

model_SVC.classes_

• Résultat de l’exécution :

• Code :

model_SVC.intercept_

• Résultat de l’exécution :

2.1.2. NuSVC

NuSVC est l’acronyme de Nu Support Vector Classification. C’est une classe fournie par la bibliothèque Scikit-learn et qui permet de faire la classification multi-classes. Le NuSVC ressemble au SVC avec une légère différence dans les paramètres.

Le NuSVC accepte un paramètre nu qui prend une valeur à virgule dans l’intervalle (0, 1] par défaut égale à 0.5 et qui représente une limite supérieure de la fraction des erreurs de training et une limite inférieure de la fraction des vecteurs de support.

Appliquons celui-ci sur la dataset « iris ».

On suit les mêmes étapes que précédemment, et on fait appel cette fois-ci à la classe NuSVC.

• Code :

from sklearn.svm import NuSVC
#instanciation
model_NuSVC = NuSVC( kernel = 'linear', gamma = 'scale', shrinking = False,)
#training
model_NuSVC.fit( x_train, y_train)
#calcule de précision
print(model_NuSVC.score( x_test, y_test))
#Prédiction
longueur = 2.5
largeur = 0.75
prediction = model_NuSVC.predict( [[longueur, largeur]])
#affichage des résultats
resultat = "Résultat : "
if prediction[0] == 0:
resultat = resultat + "setosa"
if prediction[0] == 1:
resultat = resultat + "versicolor"
if prediction[0] == 2:
resultat = resultat + "virginica"
print(resultat)


• Résultat de l’exécution :

Remarque :

Les mêmes attributs du SVC sont valables pour le NuSVC.

2.1.3. LinearSVC

Le linearSVC est similaire à un certain degré au SVC dont le noyau est linéaire (kernel = ‘linear’). La différence entre ces deux est que le linearSVC est implémenté en liblinear, le SVC, quant à lui, est implémenté enlibsvm.

Le linearSVC est plus adapté au grand nombre d’échantillons. Pour ces paramètres, il n’accepte pas le paramètre kernel car implicitement il est considéré comme étant linéaire. Il accepte en revanche les deux paramètres optionnels suivants :

- Penalty : spécifie la norme utilisée dans la pénalisation. Et qui est soit l1 soit l2.

- Loss : représente la fonction de perte.

Remarque :

Le linearSVC n’accepte pas les attributs suivants : support_, support_vectors_, n_support_, fit_status_ et dual_coef_.

Appliquons ce modèle à la dataset « iris ».

• Code :

from sklearn.svm import LinearSVC
#instanciation
model_linearSVC = LinearSVC( dual = False, random_state = 0, penalty = 'l1', tol = 1e-3)
#training
model_linearSVC.fit( x_train, y_train)
#calcule de précision
print(model_linearSVC.score( x_test, y_test))
#Prédiction
longueur = 2.5
largeur = 0.75
prediction = model_linearSVC.predict( [[longueur, largeur]])
#affichage des résultats
resultat = "Résultat : "
if prediction[0] == 0:
resultat = resultat + "setosa"
if prediction[0] == 1:
resultat = resultat + "versicolor"
if prediction[0] == 2:
resultat = resultat + "virginica"
print(resultat)


• Résultat de l’exécution :

On affiche ci-dessous le poids attribué aux caractéristiques à l’aide de l’attribut coef_. Et les valeurs constantes dans la fonction de décision en utilisant intercept_.

• Code :

model_linearSVC.coef_
model_linearSVC.intercept_


• Résultat de l’exécution :

2.2. SVM régression

Pour la régression la bibliothèque scikit-learn de Python met en place principalement les trois classes suivantes : SVR, NuSVR et LinearSVR.

2.2.1. SVR

Le SVR (Support Vector Regression) est une régression vectorielle de type Epsilon-support et est implémenté au niveau de libsvm.

SVR peut prendre le paramètre optionnel epsilon qui spécifie le tube epsilon dans lequel aucune pénalité dans la fonction de perte de training n’est associée aux points prédits à une distance epsilon de la valeur réelle. Ce paramètre prend par défaut la valeur 0.1.

Les autres paramètres et attributs sont similaires à ceux utilisés dans le SVC.

Exemple :

Prenons l’exemple suivant d’application du modèle SVR.

• Code :

from sklearn.svm import SVR
x = [[12, 12], [20,20]]
y = [1, 2]
#instanciation
model_SVR = SVR( kernel = 'linear' , gamma = 'auto')
#training
model_SVR.fit( x, y)
#Prédiction
model_SVR.predict( [[20,20]])


• Résultat de l’exécution :

Attributs 

Les mêmes attributs du SVC peuvent être utilisés par le SVR.

Ci-dessous on les applique sur le modèle de l’exemple précédent.

• Code :

model_SVR.support_
model_SVR.support_vectors_
model_SVR.n_support_
model_SVR.dual_coef_
model_SVR.coef_
model_SVR.intercept_
model_SVR.fit_status_


• Résultat de l’exécution :

2.2.2. NuSVR

Le NuSVR est la régression vectorielle de support Nu, ce modèle est similaire au NuSVC sauf que le NuSVR utilise le paramètre nu pour contrôler le nombre de vecteurs de support ainsi ce dernier remplace epsilon.

Exemple :

Dans cet exemple, on génère aléatoirement des valeurs d’échantillons et de caractéristiques à l’aide de la méthode randn() sur lesquelles s’entraine notre modèle NuSVR.

• Code :

from sklearn.svm import NuSVR
import numpy as np
echantillons = 20
caracteristiques = 15
np.random.seed(0)
x = np.random.randn( echantillons, caracteristiques)
y = np.random.randn( echantillons)
#instanciation
model_NuSVR = NuSVR( kernel = 'linear', gamma = 'auto', C = 1.0, nu = 0.1)
#training
model_NuSVR.fit(x, y)
#Prédiction
model_SVR.predict( [[20,20]])


• Résultat de l’exécution :

2.2.3. LinearSVR

LinearSVR est la régression vectorielle de support linéaire et est similaire au SVR quand le noyau est linéaire (kernel = ‘linear’). La différence entre ces deux est que le linearSVR est implémenté en liblinear, le SVRquant à lui est implémenté en libsvm.

Le linearSVCR est plus adapté au grand nombre d’échantillons. Pour ces paramètres, il n’accepte pas le paramètre kernel car implicitement il est considéré linéaire. Il accepte en revanche le paramètre optionnel :Loss qui représente la fonction de perte et prend par défaut « epsilon_insensitive ».

Remarque :

Le linearSVC n’accepte pas les attributs suivants : support_, support_vectors_, n_support_, fit_status_ et dual_coef_.

Exemple :

Dans cet exemple on importe la classe make_regression qui permet de générer un problème de régression aléatoire, sur lequel va se former notre modèle linearSVR en lui appliquant la méthode fit().

• Code :

from sklearn.svm import LinearSVR
from sklearn.datasets import make_regression
x, y = make_regression( n_features = 3, random_state = 0)
#instanciation
model_linearSVR = LinearSVR( dual = False, random_state = 0,
loss = 'squared_epsilon_insensitive', tol = 1e-5)
#training
model_linearSVR.fit( x, y)
#Prédiction
model_linearSVR.predict( [[0,0,0]])


• Résultat de l’exécution :

On affiche ci-dessous le poids attribué aux caractéristiques à l’aide de l’attribut coef_. Et la valeur constante dans la fonction de décision en utilisant intercept_.

• Code :

model_linearSVR.coef_
model_linearSVR.intercept_


• Résultat de l’exécution :

3. Cas d’utilisation 

Voici quelques exemples d’utilisation du modèle SVM :

Reconnaissances des formes :

• Reconnaissance de chiffres manuscrits.
• Reconnaissance de visages.

Diagnostic médical :

• Evaluation des risques de cancer.
• Détection d’arythmie cardiaque.

4. Avantages et limites

4.1. Avantages

Les classificateurs SVM sont d’une précision élevée et effectuent des prédictions plus rapides que d’autres modèles. Ils utilisent aussi moins de mémoire car ils utilisent un sous-ensemble de points d’entrainement dans la phase de décision.

4.2. Limites

Les SVM ne sont pas adaptés aux grands ensembles de données puisqu’ils prennent un temps de formations plus élevé. Et ils fonctionnent mal avec les classes qui se chevauchent et dépendent du noyau utilisé.

Conclusion

Dans ce tutoriel nous avons vu le SVM qui fait partie de la famille des algorithmes d’apprentissage automatique supervisés et qui permet à la fois la classification en utilisant SVC, NuSVC et linearSVC et la régression en utilisant SVR, NuSVR et linearSVR dans la bibliothèque scikit-learn de Python.