Tutoriel Python : installer et utiliser le module Math
Rédigé par Babachekhe Mohamed, Publié le 28 Octobre 2020, Mise à jour le Samedi, 14 Novembre 2020 00:35
Table des matières :
- Introduction
- le module math en python
-
Les Fonctions du module math
- Autres Fonctions importantes du module math
- Exercices
- Correction des exercices
- Conclusion
1. Introduction :
Les mathématiciens ne prouvent pas tous les théorèmes dès le déprat. Au lieu de cela, ils construisent leurs preuves sur les vérités que leurs prédécesseurs ont déjà établies. De même, il est rare que quelqu'un écrive tout seul un programme.
Un module est un ensemble de variables et de fonctions qui sont regroupées en un seul fichier. Les variables et les fonctions d'un module sont généralement liées entre eux d'une manière ou d'une autre ; par exemple, le module math contient la variable pi et les fonctions mathématiques telles que cos (cosinus) et sqrt (racine carrée). Ce tutoriel vous montre comment utiliser le module math en Python.
2. le module math en python:
La plupart des fonctions mathématiques ne sont pas intégrées dans le noyau de Python, mais sont disponibles en chargeant le module mathématique. Il y a trois façons d'accéder aux fonctions d'un module.
- Méthode 1 :
Charger toutes les définitions des fonctions du module mathématique dans la fonction courante ou module. L'utilisation de cette méthode est déconseillée car elle est non seulement source de gaspillage mais peut également entraîner des conflits avec les définitions chargées à partir d'autres modules.
Par exemple, il existe trois définitions différentes de la fonction sinusoïdale dans les modules mathématiques de Python, cmath, et Numpy Si vous avez chargé deux ou plusieurs de ces modules, il n'est pas clair quelle définition sera utilisée dans l'appel de fonction sin(x)(c'est la définition dans le module qui a été chargé en dernier).
Syntaxe :
from math import *
- Méthode 2 :
La méthode la plus sûre, mais en aucun cas infaillible, consiste à charger les définitions sélectionnées avec la déclaration:
Syntaxe :
from math import func1, func2, ...
Exemple 1:
Syntaxe:
from math import log,sin
print(log(sin(0.25)))
Résultat de l’exécution :

Les conflits peuvent être évités en rendant d'abord le module accessible avec la déclaration:
import math
et ensuite accéder aux définitions du module en utilisant le nom du module comme préfixe.
Exemple 2 :
Syntaxe:
import math
print(math.log(math.sin(0.25)))
Résultat de l’exécution :

Un module peut également être rendu accessible sous un pseudonyme. Par exemple, le module de math
peut être mis à votre disposition sous l'alias m avec la commande:
import math as m
Exemple 2 :
Syntaxe:
import math as m
print(m.log(m.sin(0.5)))
Résultat de l’exécution :

La fonction intégrée dir() renvoie une liste triée de chaînes de caractères séparées par des virgules contenant les noms des fonctions, des classes et des variables tels que définis dans le module. Par exemple, vous peut trouver toutes les fonctions supportées par le module mathématique en passant le nom du module comme un argument à la fonction dir().
Exemple 3 :
Syntaxe:
import math
dir(math)
Résultat de l’exécution :

Différentes fonctions associées au module mathématique sont affichées .
Une autre fonction intégrée que vous trouverez utile est la fonction help() qui invoque le système d'aide intégré. L'argument de la fonction help() est une chaîne de caractères, qui est recherchée comme le nom d'un module, d'une fonction, d'une classe, d'une méthode, d'un mot-clé ou d'un sujet de documentation, puis la page d'aide est imprimée dans la console. Par exemple, si vous voulez trouver des informations sur gcd() dans le module math, passez le nom de la fonction en argument sans parenthèse.
3. Les Fonctions du module math:
Les fonctions mathématiques de base apparaissent dans de nombreuses applications. Par exemple, les logarithmes peuvent être utilisés pour mettre à l'échelle des données qui croissent de façon exponentielle afin de donner des données linéaires. Les fonctions exponentielles et les fonctions trigonométriques sont courantes lorsqu’on travaille avec des informations géométriques, la fonction gamma apparaît en combinatoire, et la fonction d'erreur gaussienne est importante en statistique.
Le module math de la bibliothèque standard de Python fournissent toutes les fonctions mathématiques, ainsi que les constantes communes et certaines fonctions d'utilité.
a) Les fonctions arithmétiques du module math:
1) math.ceil(x) : Retourne la partie entière supérieure à x, le plus petit nombre entier supérieur ou égal à x.
2) math.copysign(x,y) : Retourne un float ayant la valeur absolue de x mais avec le signe du paramettre y.
3) math.fabs(x) : Retourne la valeur absolue de x.
4) math.factorial(x) : Retourne la factorielle de x. Retourne une Value Error si x n'est pas un entier ou s'il est négatif.
5) math.floor(x) : Retourne le minimum de x, le plus grand integer inférieur ou égal à x. Si x n'est pas un float, il Retourne x.
6) math.gcd(x,y) : Retourne le plus grand diviseur commun des entiers x et y Si x ou y n'est pas nul, aussi gcd(0,0) retourne 0.
7) math.modf(x) : Retourne la partie entière et la partie fractionnaire de x. Les deux valeurs ont le signe de x et sont des float.
8) math.fmod(x,y) : retourne le modulo de x par y. Remarquez que l'expression Python x % y peut ne pas retourner le même résultat. La signification du standard C pour fmod(x, y) est d'être précisément égal à x - n*y pour un integer n tel que le résultat a le signe de x et une valeur plus petite que abs(y)..
Exemple 4 :
Syntaxe:
import math
math.ceil(-4.3)
math.copysign(2,-0.1)
math.fabs(-23)
math.factorial(3)
math.floor(2.23)
math.gcd(20,4)
math.modf(4.21)
math.fmod(20,7)
Résultat de l’exécution :

b) Les Fonctions logarithme et exponentielle du module math:
1) math.exp(x) : Retourne l’exponontielle de x.
2) math.expm1(x) : Retourn exp(x) -1,mais Pour les petits nombres float, la soustraction exp(x) - 1 peut entraîner une perte importante de précision ; la fonction expm1(x) retourne cette quantité avec une précision totale.
3) math.log(x) : log(x), renvoie le logarithme naturel de x en base e.
log(x)/log(base), renvoie le logarithme de x dans la base donnée,
4) math.log1p(x) : renvoie le logarithme naturel de x+1 en base e.
5) math.log2(x) : renvoie le logarithme naturel de x en base 2 (log(x,2)).
6) math.log10(x) : renvoie le logarithme naturel de x en base 10 (log(x,10)).
7) math.pow(x,y) : renvoie x élevé à la puissance de y.
8) math.sqrt(x) : renvoie la racine carrée de x.
Exemple 5 :
Syntaxe:
import math
math.exp(-4.3)
math.expm1(2)
math.log(-23)
math.log1p(3)
math.log2(2.23)
math.log10(2)
math.pow(2,2)
math.sqrt(9)
Résultat de l’exécution :

c) Les Fonctions trigonométriques du module math:
1) math.acos(x) : renvoie l'arc cosinus de x, en radians..
2) math.asin(x): renvoie l'arc sinus de x, en radians..
3) math.atang(x) : renvoie l'arc tangent de x, en radians..
4) math.cos(x) : renvoie le cosinus de x, en radians..
5) math.sin(x) : renvoie le sinus de x, en radians..
6) math.tan(x) : renvoie le tangent de x, en radians..
7) math.atan2 (x,y) : renvoie l'arc tangent de x par y , en radians (atan(x/y).
Exemple 6 :
Syntaxe:
import math
math.acos(0.5)
math.asin(0.5)
math.atan(0.5)
math.sin(45)
math.cos(45)
math.tan(45)
math.atan2(90,2)
Résultat de l’exécution :

d) Les Fonctions hyperboliques du module math :
1) math.acosh(x) : renvoie l'arc cosinus hyperbolique de x.
2) math.asinh(x): renvoie l'arc sinus hyperbolique de x.
3) math.atangh(x) : renvoie l'arc tangent hyperbolique de x.
4) math.cosh(x) : renvoie le cosinus hyperbolique de x.
5) math.sinh(x) : renvoie le sinus hyperbolique de x.
6) math.tanh(x) : renvoie le tangent hyperbolique de x.
Exemple 7 :
Syntaxe:
import math
math.acosh(45)
math.asinh(45)
math.atanh(0.1)
math.sinh(45)
math.cosh(45)
math.tanh(45)
Résultat de l’exécution :

Le module de math offre beaucoup de fonctions trigonométriques et hyperboliques, de puissances et de logarithmes, conversions angulaires, constantes comme pi et e. Nous n'approfondirons pas la totalité car les mathématiques avancées ne sont pas si pertinentes que ça pour la plupart des gens.
4. Autres Fonctions importantes du module math:
En plus des fonctions standard telles que les fonctions trigonométriques, les logarithmes et exponentielles, le module mathématique contient un certain nombre de fonctions théoriques et des fonctions combinatoires. Il s'agit des fonctions combinatoires et factorielles, qui sont utiles dans une variété d'applications. La fonction comb appelée avec les arguments n et k renvoie le nombre de fois qu'il est possible de choisir k articles dans une collection de n sans répétition si l'ordre n'est pas important. Par exemple, prélever 1 puis 2 revient au même que prélever 2 puis 1. Ce numéro s'écrit parfois 
a) Les constantes en python :
1) math.inf : Un float infini positif. (Pour -infini ,on utilse -math.inf.).
2) math.pi: renvoie La constante ? = 3.141592…, à la précision disponile.
3) math.e: renvoie La constante e = 2.718281…, à la précision disponible.
b) Autre fonctions en python :
1) math.erf(x) : Renvoie la fonction d'erreur en x.
2) math.erfc(x) : Renvoie la fonction d'erreur supplémentaire en x.
3) math.gamma(x) : Renvoie la fonction Gamma en x.
4) math.lgamma(x): Renvoie le logarithme normal de abs(math.gamma(x)).
Exemple 8 :
Syntaxe:
import math
math.erf(23)
math.erfc(4)
math.gamma(45)
math.lgamma(34)
Résultat de l’exécution :

5. Exercices :
Exercice 1 :
Écrire 2 programmes Python un pour convertir les degrés en radian et un autre pour convertir le radian en degré.
Exercice 2 :
Écrivez un programme python pour calculer la surface d'un polygone régulier.
Exercice 3 :
Écrivez un programme Python pour calculer la distance entre deux points en utilisant la latitude et la longitude.
Exercice 4 :
Écrivez un programme Python pour calculer le volume et la surface d'un cylindre.
Exercice 5 :
Ecrire un programme Python pour trouver la racine carrée d'un nombre en utilisant les fonctions sqrt et pow.
6. Correction des exercices :
Exercice 1 :
Syntaxe:
#programme 1
import math
degree = float(input("enter degrees: "))
radian = degree*(math.pi/180)
print("radian: ",radian)
#programme 2
import math
radian = float(input("entre radians: "))
degree = radian*(180/math.pi)
print("degre: ",degree)
Résultat de l’exécution :

Exercice 2 :
Syntaxe:
import math
n_cote = int(input("Saisie du nombre de côtés : "))
s_longeur = float(input("Saisir la longueur d'un côté: "))
S= n_cote * (s_longeur ** 2) / (4 * math.tan(math.pi / n_cote))
print("la surface du polygonne est : ",S)
Résultat de l’exécution :

Exercice 3 :
Syntaxe:
import math
print("Saisie des coordonnées de deux points:")
slat = math.radians(float(input("Latitude de départ: ")))
slon = math.radians(float(input("Fin de la longitude: ")))
elat = math.radians(float(input("Latitude de départ: ")))
elon = math.radians(float(input("Fin de la longitude: ")))
dist = 6371.01 * math.acos(math.sin(slat)*math.sin(elat) + math.cos(slat)*math.cos(elat)*math.cos(slon - elon))
print("La distance est %.2fkm." % dist)
Résultat de l’exécution :

Exercice 4 :
Syntaxe:
import math
height = float(input('Hauteur du cylindre: '))
r = float(input('Rayon du cylindre: '))
volume = math.pi * r * r * height
s = ((2*math.pi*r) * height) + ((math.pi*r**2)*2)
print("le volume est: ", volume)
print("la Surface est: ", s)
Résultat de l’exécution :

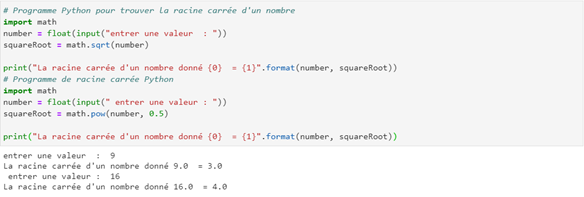
Exercice 5 :
Syntaxe:
# Programme Python pour trouver la racine carrée d'un nombre
import math
number = float(input("entrer une valeur : "))
squareRoot = math.sqrt(number)
print("La racine carrée d'un nombre donné {0} = {1}".format(number, squareRoot))
# Programme de racine carrée Python
import math
number = float(input(" entrer une valeur : "))
squareRoot = math.pow(number, 0.5)
print("La racine carrée d'un nombre donné {0} = {1}".format(number, squareRoot))
Résultat de l’exécution :
7.Conclusion :
Le module mathématique contient des fonctions qui sont implémentées en C (en supposant que vous êtes tournant sous CPython), et sont donc beaucoup plus rapides que celles implémentées en Python. C'est un bon choix si vous devez appliquer une fonction à une collection de numéros. Si vous souhaitez appliquer ces fonctions à une grande collection, il est préférable d'utiliser leurs équivalents du paquet NumPy. En général, si vous avez importé le paquet NumPy, alors il est préférable d'utiliser les fonctions équivalents de NumPy pour limiter le risque d'erreur.
