Formation Matlab pour débutant

Formation Matlab
ENSEIRB, FILIERES ELECTRONIQUE ET TELECOMMUNICATIONS, 1ERE ANNEE ANNEE 2005-2006
TABLE DES MATIERES
NOTE TECHNIQUE : LANCEMENT DE MATLAB SOUS WINDOWS ET SOUS UNIX: . 4
PARTIE N° 1MATLAB : COMMANDES DE BASE ET INTRODUCTION AUX CALCULS
MATRICIELS 5
1.1 DESCRIPTION DE LA FENETRE DE COMMANDE DE MATLAB . 5 1.2 EXPLORATION DES BIBLIOTHEQUES 7
1.2.1Matlab et ses bibliothèques . 71.2.2Commande help . 81.2.3Commande lookfor .. 81.2.4Localisation de la fonction utilisée . 91.2.5Autres commandes .. 9
1.3 COMMANDES DE GESTION DE L’ESPACE DE TRAVAIL . 9
1.3.1Introduction . 91.3.2Matlab comme simple calculateur 101.3.3Nombre complexe .. 111.3.4Mathématiques, géométrie 111.3.5Ecriture directe d’une matrice ou d’un vecteur . 111.3.6Gestion des variables dans l’espace de travail : commandes whos, clear, format .. 12 1.4 OPERATIONS DIRECTES SUR LES MATRICES .. 13
1.4.1Opérations arithmétiques : 131.4.2Opérations relationnelles et logiques .. 13 1.5 MANIPULATIONS SUR LES ELEMENTS MATRICIELS 13
1.5.1Manipulation des indices .. 131.5.2Valeurs particulières 14
1.6 MATRICES CREUSES (HELP SPARFUN) 14 1.7 MATRICE ET CHAINE DE CARACTERES 14 1.8 BILAN ET EXERCICE D’APPLICATION 15
1.8.1Ce qu’il faut (au minimum) retenir ! 15
1.8.2Exercice d’application 1 16
PARTIE N° 2SUR CERTAINES FONCTIONS DEDIEES AU CALCUL .. 17
2.1 INITIALISATION ET MANIPULATION .. 17 2.2 ALGEBRE LINEAIRE .. 18 2.2.1Fonctions élémentaires .. 182.2.2Fonctions de décomposition . 18 2.3 OPERATIONS SUR LES DONNEES . 19
2.3.1Génération aléatoire 19
2.3.2Analyse des données . 19 2.4 OPERATIONS SUR LES POLYNOMES .. 19 PARTIE N° 3ÉLEMENTS DE PROGRAMMATION . 21
3.1 INTRODUCTION .. 21 3.2 SCRIPT 21
3.2.1Définition d’un script .. 213.2.2Construction d’un script . 21 3.3 FONCTIONS .. 22
3.3.1Introduction .. 223.3.2Définition .. 223.3.3Exemple de fonction . 23
3.4 STRUCTURES DE PROGRAMMATION USUELLES 23 3.4.1Structure de type test 24
3.5 BILAN ET EXERCICES D’APPLICATION : CREATION D'UNE FONCTION .. 26 PARTIE N° 4GRAPHISME .. 27
4.1 PREAMBULE . 27 4.2 NOTION DE FIGURE .. 27 4.3 AFFICHAGE DES COURBES 2D . 28
4.3.1Commande plot .. 28
4.3.2Commande fplot . 294.3.3Commande subplot 294.3.4Commande axis .. 30
4.4 AFFICHAGE DES COURBES 3D . 30
4.4.1plot3 : arguments vectoriels . 304.4.2Fonctions à arguments matriciels . 314.4.3meshgrid . 314.4.4plot 324.4.5contour et contour3 .. 334.4.6mesh et surf .. 334.4.7image 344.4.8colormap et colorbar 344.4.9view .. 35 4.5 GRAPHES SPECIALISES 36
4.5.1Barres et surfaces .. 364.5.2Camemberts .. 36
4.6 EXERCICE : GRAPHISME ET FONCTIONS .. 37 4.7 AUTRE EXERCICE .. 38 4.8 EXERCICE IMAGES 38 PARTIE N° 5FICHIERS DE DONNEES .. 39 5.1 FICHIERS MATLAB 39
5.1.1Commande save . 395.1.2Commande load . 39
5.2 FICHIERS BINAIRES ET ASCII: LE FORMAT STANDARD 40
5.2.1Commande fopen 405.2.2Commande fread 415.2.3Commande fwrite .. 425.2.4Commande fclose .. 425.2.5Commande fprintf .. 42 5.3 EXERCICE . 42 PARTIE N° 6APPLICATIONS 43
6.1 RAPPELS SUR LE DEVELOPPEMENT EN SERIE DE FOURIER ET TRANSFORMEE DE FOURIER 43
6.2 EXERCICE . 45 6.2.1Décomposition en série de Fourier, représentation spectrale et somme de série . 45
INTRODUCTION
L’objectif de cette formation est de se familiariser au logiciel Matlab, applicatif dédié au calcul scientifique le plus utilisé dans les laboratoires universitaires et industriels tel que le CEA, Thomson, le CNES, etc.
A l’origine, la toute première version de Matlab fut mise en œuvre aux Universités du Nouveau Mexique et de Stanford, à la fin des années 70. Elle se destinait essentiellement à l’analyse numérique et à l’algèbre linéaire. Depuis, Matlab est devenu un outil que l’on peut utiliser pour mener des simulations dans de très nombreux domaines (traitement du signal, traitement d’image, automatique, statistique, aéronautique, etc.) et pour développer des applications avec une interface graphique.
Cette formation traite plus particulièrement la déclaration et la gestion des données (matrice, chaîne de caractères, etc.), la création d’un programme et la gestion d’un espace de développement, la création de fonctions et gestion des bibliothèques et des fichiers de données.
Ce logiciel sera en outre utilisé tout au long de votre formation à l’école et dans l’industrie, notamment sur des thèmes liés aux probabilités, processus aléatoires, filtrage et plus généralement le traitement du signal et des images ainsi que l’automatique.
Note technique : Lancement de Matlab sous Windows et sous UNIX:
A l'ENSEIRB, Matlab est installé à la fois sous Windows et sous UNIX. La procédure de lancement est différente dans les deux cas.
Sous Windows, Matlab se trouve dans le menu Démarrer.
Sous UNIX, il faut le lancer à partir de la ligne de commande. La procédure à suivre est la suivante:
• Avant de vous loguer, assurez vous que le terminal est en mode graphique 24 bits. Pour cela, entrez votre login, puis ouvrez le menu "Option" de l'écran de login, et choisissez "Session" puis "Switch 24 bit plans". Validez votre mot de passe. L'écran devrait clignoter, puis l'écran de login réapparaît. Rerentrez votre login en choisissant cette fois un type de session classique (par exemple "Gnome 2.0"). Le mode 24 bits permet aux applications de bénéficier de millions de couleur pour l'affichage, alors que le mode 8 bits ne permet que 256 couleurs distinctes. Lorsque Matlab est lancé alors que le moniteur est en mode 8 bits, il affiche un message d'avertissement indiquant que le nombre de couleurs disponibles est insuffisant. Cela ne pose aucun problème, à part le fait que les couleurs peuvent apparaître fantaisistes dans les fenêtres qui ne sont pas actives. Utilisez la procédure décrite précédemment si cela vous gêne.
• Dans un terminal, tapez le chemin d'accès complet vers l'exécutable Matlab, puis validez. Selon la version désirée, (Matlab 6.5 ou Matlab 7), le chemin est différent. D'une manière générale, Matlab 6 est plus rapide et Matlab 7 offre plus de fonctionnalités en terme d'interface graphique. Les chemins d'accès sont: o /opt/matlab/bin/matlab pour Matlab 6.5
o /opt/matlabr14/bin/matlab pour Matlab 7
Le lancement de Matlab sous UNIX peut prendre un peu de temps, car le logiciel doit être chargé à travers le réseau. Une fois lancé, il devrait cependant réagir normalement. Soyez patients.
Si Matlab génère une erreur de license au démarrage due au gestionnaire de licenses FlexLM, cela peut être du à
• Nombre trop important de personnes utilisant Matlab en parallèle
• Problème d'accès au gestionnaire de licenses si vos variables d'environnement sont mal configurées. Tapez la commande suivante avant de réessayer : o source /opt/matlab/ENSEIRB.README
PARTIE N° 1MATLAB : COMMANDES DE BASE ET INTRODUCTION AUX CALCULS MATRICIELS
1.1Description de la fenêtre de commande de Matlab
Lancer Matlab, en utilisant le menu démarrer. Selon les versions du logiciel, on obtient l’un des deux fenêtres de commande suivantes. Le chargé de cette formation montrera éventuellement la mise en œuvre d’un raccourci. Avec la version précédente, on a :
A partir des versions 6 et 7, la fenêtre de commande ("prompt") est complétée par des fenêtres utilitaires permettant de visualiser les fichiers du répertoire courantou les variables définies dans le workspace courant, ce qui correspond aux commandes ls et whos.
Il existe quatre menus déroulants :
- File : le menu fichier permet notamment d’accéder à des fichiers déjà existants ou de créer de nouvelles procédures et des nouveaux programmes. Il permet aussi de quitter Matlab. Les derniers programmes ouverts sont en outre indiqués.

- Edit : le menu édition permet d’accéder aux commandes classiques : copier, couper, coller, sélectionner tout, etc.
- Window : le menu Fenêtre donne accès aux différentes fenêtres de Matlab ouvertes.
- Web : spécifique à Matlab 6.1.
- Help : c’est le menu d’aide.
Le soulignement des lettres F, E, W et H des menus File, Edit, Window, Help indique le raccourci clavier pour ouvrir le menu déroulant sans l’aide de la souris. On effectue alors la commande alt+lettre soulignée.
Comme dans les logiciels Word et Excel, on peut aussi exploiter la barre d’outils. Cette dernière comprend plusieurs « boutons » qui permettent notamment de créer une nouvelle fenêtre d’édition pour l’écriture de programmes, d’ouvrir un fichier déjà existant, de couper, copier ou coller une partie d’un programme, d’annuler la dernière action, etc.
Il est à noter qu’une information « bulle » apparaît lorsque la souris est positionnée suffisamment longtemps sur l’un des boutons ; elle renseigne alors sur son rôle.
On constate aussi que la fermeture × et la mise en icône - de la fenêtre de commande peut se faire par un simple clic sur les boutons de gestion de fenêtre, situés en haut à droite. La fenêtre peut aussi couvrir la totalité de l’écran, puis reprendre sa taille initiale, à l’aide du dernier bouton.
Le déplacement de la fenêtre s’effectue en maintenant le bouton d’action de la souris (en général celui de gauche) sur la barre descriptive de la fenêtre.
Enfin, la fenêtre dispose de barres de défilements vertical et horizontal. Comme pour Word, Excel, Powerpoint, etc., le « dimensionnement » de la fenêtre est possible. On se place alors à la limite de la fenêtre et en maintenant le bouton d’action enfoncé de la souris, on définit une nouvelle taille de la fenêtre.
En outre, le prompt de Matlab est défini par le sigle >>.
Application : On propose, en guise de préambule, de manipuler la démonstration pour connaître les possibilités qu’offre le logiciel Matlab. Pour accéder à la démonstration, il suffit de taper demo dans la fenêtre de commande, ce qui fait apparaître des fenêtres interactives donnant un panorama des différents outils proposés par le logiciel. On peut en général y lire les principales lignes de programmes.
Exploration des bibliothèques
1.2.1 Matlab et ses bibliothèques
Matlab est un logiciel qui dispose d’une collection de fonctions/programmes, que l’on désigne aussi par des fichiers à extension .m. Ces .m sont classés par thèmes et constituent alors des boîtes à outils (ou toolboxes en anglais). On dispose ainsi des toolboxes ‘general’, ‘identification’, ‘signal’, etc. Matlab ayant été créé à partir d’une bibliothèque dédiée au calcul matriciel, de nombreuses bibliothèques sont relatives à l’algèbre linéaire (‘elmat’, ‘specmat’, ‘matfun’).
Ces bibliothèques sont mises en place au moment de l’installation de Matlab. Il est à noter qu’elles sont payantes. Mais elles sont très utiles car elles regroupent des traitements de bases (par exemple, le calcul du déterminant d’une matrice, l’obtention des valeurs propres ou singulières et des vecteurs associés, etc.). En général, chaque programme débute par un commentaire de quelques lignes décrivant l’objectif du programme, les entrées, etc.
Comme les bibliothèques doivent être accessibles de n’importe quel point où l’on se place dans l’arborescence du disque, une variable PATH doit être configurée pour définir les chemins d’accès. L’ensemble des liens vers des bibliothèques existantes est disponible en tapant dans la fenêtre de commandes : path.
On peut sinon créer des bibliothèques personnelles contenant ses propres fonctions ou d’autres trouvées sur le net. Pour cela, il faut définir des répertoires où elles seront placées. De la même manière que précédemment, il faut configurer une variable PATH.
Pour cela, on suit la procédure suivante :
- création d’un répertoire associé à la bibliothèque nom_lib ;
- création du fichier startup.m qui va contenir la mise à jour du path général de Matlab : path(‘/home/Matlab/nom_lib’,PATH);
Application : Créer un répertoire de travail à partir du « poste de travail » de votre ordinateur puis votre bibliothèque personnelle nommée libpers. Attention : ne pas oublier de remplacer le chemin /home/Matlab/nom_lib par celui adapté à votre cas !
Pour explorer les bibliothèques, deux commandes help et lookfor associés à un mot clé peuvent être exploitées.
Commande help
Un champ de description est associé à chaque fonction ; grâce à la commande help, on obtient à l’écran un texte qui permet de savoir à quoi sert la fonction, mais aussi comment l’employer. Cette commande peut s’utiliser à deux niveaux :
- la commande help sans argument donne le listing des bibliothèques où sont regroupées les fonctions par type ;
- la commande help "Topic" fournit les renseignements sur les bibliothèques ou sur les fonctions selon que Topic équivaut à une bibliothèque ou à une fonction.
Exemple : si l’on tape helpcos, on obtient une description de la fonction cos.
Figure n°2 : utilisation de la commande help
Application : lire les descriptions des fonctions cos, det, eig, butter et plot.
Commande lookfor
En utilisant la commande lookfor, on effectue une recherche par thème qui renvoie le nom de chaque fonction associée à ce thème et ses différents arguments.
Exemple : si l’on tape lookfor inverse, on obtient un listing des fonctions ayant le mot inverse dans leur texte de description (en anglais en général).
Application : rechercher la commande qui permet de réaliser l’affichage d’un titre pour un graphe.
Figure n°3 : utilisation de la commande lookfor
1.2.4 Localisation de la fonction utilisée
Après avoir vu les commandes permettant de connaître les fonctionnalités des outils proposées par Matlab, il peut être utile de localiser la fonction étudiée sur le disque. Pour cela, on utilise la commande : whichnom_function
Application : à quelles bibliothèques appartiennent les fonctions cos, det, eig, butter?
1.2.5 Autres commandes
| fonctions | définition |
| pwd | indique le répertoire de travail |
| cd | permet le déplacement dans l’arborescence du disque |
| ls | description du contenu du répertoire |
1.3Commandes de gestion de l’espace de travail
1.3.1 Introduction
Comme un calculateur, Matlab peut effectuer des opérations simples : une addition, une multiplication, une soustraction, une division, une mise à la puissance d’un nombre. L’objet de cette partie est tout d’abord d’effectuer ces opérations élémentaires puis d’introduire la notion de variables et de calculs mathématiques.
1.3.2 Matlab comme simple calculateur
Prenons un exemple simple : Yannick et Eric, « deux grands sportifs », décident de jouer au tennis pendant deux heures dans un club des Landes. Ils n’ont malheureusement pas de matériel et décident de louer les raquettes et les balles. La location d’une raquette est de 15 F pour une heure. La boite de balle est louée 10 F pour la totalité de la partie et la location du court à l’heure est de 60 F.
Dans la fenêtre de commande, on peut immédiatement résoudre ce problème en tapant >>4*15+10+2*60
En tapant sur entrée, le résultat s’affiche.
Il est à noter que la présence d’espace ou non entre les opérateurs n’influe pas sur le résultat, noté ans par défaut par Matlab. L’ordre des opérations se fait de gauche à droite et suit l’ordre habituel des règles de priorités. La multiplication (*) et la division (/ ou \ ; 100/2=2\100) sont prioritaires devant l’addition (+) et la soustraction (-). La mise à la puissance (^) a l’ordre de priorité le plus élevé. Les parenthèses s’emploient elles aussi de façon classique.
Le problème que l’on vient de traiter peut se résoudre d’une autre manière en stockant les données dans des variables. Ainsi, on peut noter raq la variable relative au prix de la location d’une raquette, nbre_raq le nombre de raquette, balle le prix de la location de la boite de balles, court la location du court à l’heure et heure le nombre d’heures passées sur le terrain. On entre alors les valeurs variables une après l’autre comme suit :
>>raq=15 puis taper entrée !
Application : entrer toutes les variables et calculer le prix total que l’on stocke dans la variable prix.
Le nom des variables peut contenir jusqu’à 31 caractères. Ils doivent nécessairement commencer par une lettre et peuvent être suivis par des chiffres ou le caractère _. Les caractères de ponctuation ne sont pas acceptés. Matlab fait la différence entre minuscule et majuscule.
| Remarque : | on peut valider les opérations en appuyant à chaque fois sur entrée ou les écrire sur une même ligne mais en les séparant par une virgule. |
| Remarque 2 : | si une commande est suivie d’un point virgule, le résultat n’apparaît pas sur la fenêtre de commande mais la commande a été effectuée. |
| Remarque 3 : | rappel des dernières commandes tapées dans la fenêtre de commandes : au lieu de réécrire une commande déjà effectuée, on peut exploiter les touches du clavier ? et ? pour la rappeler. Il faut cependant que le curseur soit positionné après le prompt. Après un emploi important de la fenêtre de commande, on peut accélérer la recherche de la commande, en écrivant après le prompt (>>), la première lettre de la commande souhaitée. |
| Remarque 4 :  | pour effectuer un commentaire, on commence par %. |
| Remarque 5 : | on peut enfin exploiter les … pour signifier à Matlab que le reste de la commande apparaît à la ligne suivante. |
Remarque 6 : On peut enfin interrompre Matlab à n’importe quel moment en appuyant sur Ctrl+C.
1.3.3 Nombre complexe
Pour définir la partie imaginaire d’un nombre complexe, on multiplie par i ou par j. Pour extraire la partie imaginaire et la partie réelle d’un nombre complexe, on emploie respectivement les fonctions imag et real. Le calcul du module se fait avec la fonction abs. Enfin, si l’on souhaite passer à une représentation en coordonnées polaires du nombre complexe, la détermination de l’angle s’effectue à l’aide de la fonction angle.
Application : entrer la variable comp égale à 1-2i. Retrouver sa partie réelle, sa partie imaginaire et sa représentation en coordonnées polaires.
1.3.4 Mathématiques, géométrie
| fonctions | définition |
| abs(x) | valeur absolue ou module d’un nombre complexe |
| acosh(x) | fonction inverse du cosinus hyperbolique |
| asin(x) | fonction inverse du sinus |
| asinh(x) | fonction inverse du sinus hyperbolique |
| atan(x) | fonction inverse de la tangente |
| atanh(x) | fonction inverse de la tangent hyperbolique |
| conj(x) | complexe conjugué |
| cos(x) | cosinus |
| cosh(x) | cosinus hyperbolique |
| exp(x) | fonction exponentielle |
| floor(x) | partie entière dans le cas d’un réel positif |
| imag(x) | partie imaginaire |
| log(x) | fonction logarithme népérien |
| log10(x) | fonction logarithme en base 10 |
| real(x) | partie réelle |
| sign(x) | fonction signe |
| sin(x) | sinus |
| sinh(x) | sinus hyperbolique |
| sqrt(x) | racine carrée |
| tan(x) | tangente |
| tanh(x) | tangente hyperbolique |
L’une des bibliothèques les plus employées est celle qui contient les fonctions mathématiques géométriques les plus usuelles. Le tableau donné précédemment regroupe les principales fonctions prédéfinies relatives à ce thème.
1.3.5 Ecriture directe d’une matrice ou d’un vecteur
Pour définir une matrice sous Matlab, on suit les conventions suivantes :
- séparer les éléments d’une même ligne par un blanc ; - utiliser le symbole (;) pour indiquer la fin d’une ligne ;
- définir le début et la fin de la matrice par des crochets [ ] ;
??3 3?
Application : Entrer la matrice A = ? ? et le scalaire d=3.
? 4 5?
1.3.6 Gestion des variables dans l’espace de travail : commandes whos, clear, format
La commande whos donne la liste des variables avec leurs caractéristiques définies dans l’espace mémoire. Les commandes clear et format permettent respectivement de détruire une variable de l’espace de travail et donne la possibilité de modifier le format d’affichage des variables qui sont restituées à l’écran.

Application : Détruire toutes les variables sauf la matrice A et le scalaire d. Puis, définir une variable scalaire complexe b en entrant >>b =1+i*10 ; et taper la commande whos. Le résultat est le suivant :
Figure n°4 : utilisation de la commandewhos
Si l’on souhaite utiliser la valeur ?, on tape pi (en minuscules).
Application 2 : modifier le format d’affichage de la valeur ?.
Figure n°5 : utilisation de la commandeformat
1.4Opérations directes sur les matrices
1.4.1Opérations arithmétiques :
Les opérations sur les matrices se font en écriture directe à l’aide des opérateurs *, /, \, +, etc.
Application : une fois toutes les variables déjà existantes détruites, utiliser la fenêtre de
??3 3? ?5? ?4?
commandes pour définir : A = ? ? x =??2??y = ??1?? .
?4 5?
| Calculer: | |
| w = A*x | (vecteur) |
| sd = w'*y | (scalaire) . ’ permet de calculer la transposée de la matrice. |
| h= w? y | (vecteur) |
| z = w.* y | (vecteur) . .* permet d’effectuer une multiplication terme à |
terme.
1.4.2 Opérations relationnelles et logiques
| fonctions | définition |
| < > | différent de |
| <= >= | inférieur (supérieur) ou égal |
| == | égal |
| ~= | différent |
| & | et logique |
| | | ou |
| ~ | complément logique (not) |
| xor | ou exclusif |
1.5Manipulations sur les éléments matriciels
1.5.1 Manipulation des indices
- Lecture d’un élément :
A(i,j) permet de voir l’élément à la ième ligne et la jème colonne de A ; - Modification d’un élément :
A(i,j)=d
- Lecture d’une ligne ou d’une colonne :
A(i,:) renvoie la ième ligne de A.
A(:,j) renvoie la jème colonne de A - Suppression de la ième ligne :
A(i,:)=[]
Attention: après la suppression, les numéros de lignes seront décalés.
- Concaténation de deux matrices:
B=[A,C] ou B=[A C] : concaténation horizontale: la matrice C est ajoutée à droite de la matrice A
B=[A;L] : concaténation verticale, la matrice L est ajoutée au bas de la matrice A
Si l’on désire insérer une colonne (resp. une ligne) dans une matrice, cela revient en fait à concaténer deux matrices dont l'une est un vecteur colonne (resp. ligne). On ne peut pas insérer simplement une colonne ou une ligne à l'intérieur d'une matrice.
Application : ajouter à la matrice A une ligne dont les éléments sont [10 -2]. Puis, modifier la valeur de l’élément (3,2), en lui donnant une nouvelle valeur égale à -205.
1.5.2 Valeurs particulières
Deux valeurs informatiques non définies sont manipulées par Matlab : NaN (Not a number) représente l’élément non défini et Inf est associé à l’infini.
Application : en posant x =[8 0 0] et y =[4 0 5] calculer d = y./ x
Remarque : les fonctions isnan et isinf permettent de savoir si dans une matrice les éléments NaN et inf sont présents.
1.6Matrices creuses (help sparfun)

Les matrices creuses (sparse matrix) sont des matrices caractérisées par un nombre très important d’éléments nuls. D’un point de vue informatique, un traitement particulier de ces matrices permet un gain en place mémoire et en coût calculatoire.
| fonctions | définition | |
| sparse | création d’une matrice creuse | |
| full | conversion d’une matrice creuse | |
| issparse | retourne 1 si la matrice est creuse | |
| speye | matrice identité creuse |
Application : Créer une matrice aléatoire de taille 6×6, notée A avec la fonction rand. Générer la matrice B ne contenant que les éléments supérieurs à 0.92 et des zéros ailleurs (A>0,92).*A. Cette matrice est alors transformée en matrice creuse en utilisant les fonctions adaptées. Vous vérifierez le résultat avec la commande whos.
Remarque : on verra dans la partie 2 que la fonction rand permet la génération de processus aléatoire
1.7Matrice et chaîne de caractères
Dans Matlab, les chaînes de caractères sont des matrices. Elles sont définies par des guillemets simples : 'entre guillemets simples' .
Remarque: Il ne s'agit pas des guillemets inversés : `pas de guillemets inversés`, ni de guillemets doubles : "pas de guillemets doubles".
Figure n°6 : exemple sur les chaînes de caractères
Les fonctions associées se trouvent dans la toolbox « strfun ». (help strfun). On y trouve les fonctions de conversion, de comparaison, de recherche, etc.
1.8Bilan et exercice d’application
1.8.1Ce qu’il faut (au minimum) retenir !
Matlab est un logiciel qui dispose d’une collection de bibliothèques contenant des fonctions/programmes extension .m. Comme un calculateur, Matlab peut effectuer des opérations simples et peut stocker des variables de nature différentes (matrice, vecteur, scalaire, réel, complexe, etc.).
Parmi les commandes à connaître : path, help, lookfor, which, pwd, cd, ls, whos, clear, format, etc.
On peut interrompre Matlab à n’importe quel moment en appuyant sur Ctrl+C.
1.8.2 Exercice d’application 1
| - | ?16 ? Créer la matrice suivante A = ? 3 ? 2 ? ?13 | 5 10 11 8 | 9 6 7 12 | 4 15 14 1 | ?1? ? 2 ? 17? ? 4 ? |
- Créez une matrice B={bij } de la même taille que A={aij }, et pour laquelle bij=1 si 6 ? aij ? 11, et bij=0 sinon.
- Rechercher les éléments de la matrice A={aij } qui obéissent à la relation 6 ? aij ? 11.
On utilisera pour cela la fonction find, qui permettra de déterminer les éléments de la matrice B égaux à 1.
- Calculer la somme de la diagonale commençant par l’élément a1,2 . On utilisera pour cela les fonctions diag et sum.
- Calculer le déterminant de la matrice A * AT *a1,2 . On utilisera pour cela la fonction det.
- Générer à l’aide de la fonction rand une matrice D dont les éléments sont aléatoires de taille (4×4). Créer une matrice binaire à l’aide des opérateurs relationnels correspondant aux éléments de D qui sont supérieurs à 0.2 et inférieurs à 0.8. Créer alors la matrice G qui ne contient que les éléments de D donnés par les inégalités et des zéros ailleurs.
PARTIE N° 2SUR CERTAINES FONCTIONS DEDIEES AU CALCUL
2.1 Initialisation et manipulation
Deux fonctions permettent de générer des matrices initialisées à zéro ou à une valeur quelconque.
| fonctions | définition  | |
| zeros | remplissage de zéros | |
| ones | remplissage de 1 | |
| eye | matrice identité |
Application : Créer un vecteur ligne contenant successivement douze 0, puis huit 1 et enfin douze 0.
Application 2 : Créer les matrices suivantes à l’aide des fonctions zeros, ones et eye, et en les concaténant horizontalement ou verticalement de façon appropriée.
| ? 0 ? ? 0 ? 0 ? ?? 0.2 | 1 0.1 | 1 0.2 | 0 ? ?1 ? ? 0 ? , ?0 1 ? ?0 ? ? ? 0.05 ? ?1 | 1 1 | 1 1 | 0? ? 1? . 1? ? 0? |
Différentes fonctions permettent de modifier l’organisation des éléments d’une matrice à partir de rotations ou de symétries.
| fonctions | définition | |
| flipud | symétrie horizontale (up-down) | |
| fliplr | symétrie verticale (left-rigth) | |
| triu | partie triangulaire supérieure | |
| tril | partie triangulaire inférieure | |
| sort | arrangement par ordre croissant | |
| rot90 | rotation de 90° |
Application : A partir d’une matrice de taille 4*4, opérer successivement sur cette même matrice une rotation de 90° puis une symétrie verticale.
2.2 Algèbre linéaire
De nombreuses fonctions relatives à l’algèbre existent dans Matlab. Cet outil a été développé en effet dans le contexte de l’algèbre dans ses versions préliminaires. Notre objectif n’est pas de fournir un descriptif exhaustif de toutes les fonctions. On se limite à certain nombre afin de proposer un point d’entrée à l’utilisateur.
2.2.1 Fonctions élémentaires
Les fonctions élémentaires regroupent les fonctions qui restituent une grandeur relative à la matrice étudiée.
| fonctions  | définition | ||||||
| trace | trace de la matrice | ||||||
| det | déterminant | ||||||
| norm | normes 1, 2 etc. de la matrice | ||||||
| cond | conditionnement | ||||||
| rank | rang | ||||||
| Application : | ?1 Calculer le rang de la matrice ? ?2 | 2 4 | ? 1 ? 2 | 2? ? . 4? | |||
2.2.2 Fonctions de décomposition
De nombreuses techniques de décomposition existent dans l’algèbre linéaire. Ces décompositions se retrouvent à travers les fonctions suivantes :
| fonctions | définition | ||
| eig | décomposition en éléments propres | ||
| svd | décomposition en éléments singuliers |
Application : Calculer les valeurs singulières associée à la décomposition SVD de la matrice A donnée par la relation A=UDVT
| ?2 A = ??3 ??4 | 1 2 | ? 1 6 1 | 2? ? 5? 8?? |
Vérifier que l’on a les valeurs propres de la matrice AAT qui correspondent aux valeurs singulières élevées au carré.
2.3Opérations sur les données
2.3.1 Génération aléatoire
La génération de processus aléatoires est possible sous Matlab avec les deux fonctions qui suivent :
| fonctions | définition |
| rand | remplissage de valeurs aléatoires : distribution uniforme |
| randn | remplissage de valeurs aléatoires : distribution gaussienne |
2.3.2 Analyse des données
Certaines de ces fonctions sont relatives à la caractérisation d’un processus aléatoire. Elles permettent toutes de caractériser le jeu de données qui est en entrée.
| fonctions | définition | |
| median | valeur médiane 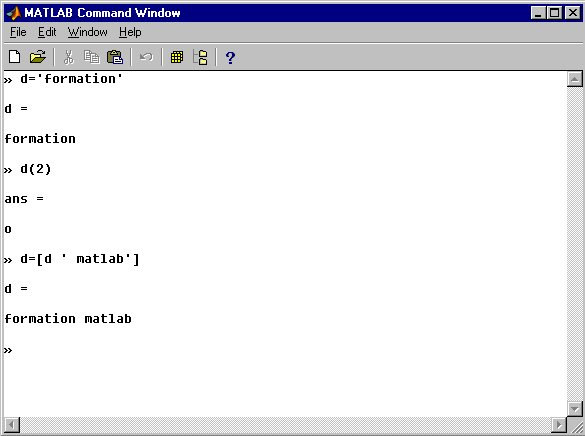 | |
| max | maximum | |
| min | minimum | |
| std | écart type (standard deviation) Cf. cours de probabilités, processus aléatoires | |
| mean | moyenne | |
| corrcoef | coefficient de corrélation Cf. cours de probabilités, processus aléatoires | |
| prod | produit des éléments | |
| sum | somme des éléments |
Application : Générer à l’aide de la fonction rand 15 échantillons d’un processus aléatoire de distribution uniforme. Calculer sa moyenne et sa variance. En outre, extraire la valeur max et min du jeu de données en incluant l’information relative à leur position dans le vecteur.
2.4Opérations sur les Polynômes
Les différentes fonctions présentées dans ce paragraphe sont relatives aux polynômes, ces polynômes sont gérés sous Matlab en suivant un ordre décroissant pour l’exposant et donc pour la déclaration de leurs coefficients.
| fonctions | définition | |
| roots | Calcul des racines connaissant les coefficients | |
| poly | Calcul des coefficients connaissant les racines | |
| polyval | Calcul de P(x) | |
| polyfit | Identification des coefficients d’un polynôme à l’aide des moindres carrés | |
| conv | Produit de deux polynômes | |
| deconv | Division de deux polynômes |
Application : Déterminer les coefficients du polynôme caractérisé par les racines A = [0,5 2 4,3]. Calculer la valeur prise par P(x) pour x = ?2 .
Application 2 Evaluer les coefficients du polynôme caractéristique associé à la matrice
?2 ? 1?
A = ? ? .
?3 7 ?
PARTIE N° 3ÉLEMENTS DE PROGRAMMATION
3.1Introduction
Après avoir vu un certain nombre de commandes utilisées directement sous le prompt de Matlab, on s’intéresse maintenant à la construction de programmes contenant plusieurs commandes. La programmation sous le logiciel Matlab conserve l’esprit de simplicité à savoir une programmation directe sans pointeur ou autre. Pour développer une application, deux éléments sont donc à considérer :
1. le programme principal appelé "script".
2. les éléments de type fonction ou sous-fonction.
3.2Script
3.2.1 Définition d’un script
Un programme Matlab est un fichier texte contenant un certain nombre de commandes Matlab. Sur le disque, il apparaît toujours de la façon suivante : nom_script.m
Ce programme s’écrit à l’aide d’un éditeur de texte quelconque. Par défaut, vous avez celui proposé par Matlab mais il peut être modifié à l’aide du menu préférences.
3.2.2 Construction d’un script
Leur construction est très simple. En fait, il s’agit d’une succession de commandes dans un fichier texte, celles-ci même que l’on entrait précédemment sous le prompt. Pour réaliser un bon script, les trois points suivants doivent être respectés :
1. Pour plus de sécurité, toujours débuter un script par la commande clear pour que les données contenues dans l’espace de travail n’interfèrent pas avec les variables utilisées dans le script.
2. Créer une zone de commentaires. En effet, pour réaliser une bonne gestion de ses programmes, il est utile de leur associer un commentaire détaillant leur fonctionnement. Pour chaque ligne de commentaire, le sigle % doit être tapé au début de chaque ligne. Il est à noter que ces commentaires sont accessibles avec la commande help.
3. Comme Matlab est un langage pré-compilé, il faut être rigoureux dans sa programmation en vue d’une économie de temps de traitement.
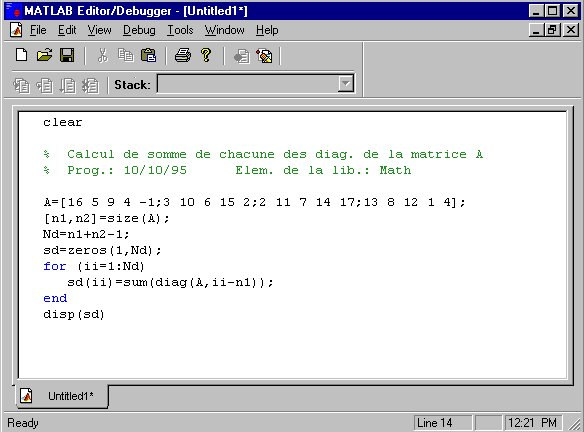
Application : calcul des sommes des éléments de chacune des diagonales d’une matrice.
Une fois le script écrit et enregistré, on peut l’exécuter en tapant sur la fenêtre de commande le nom du programme.
3.3Fonctions
3.3.1 Introduction
Les fonctions ont un rôle très important dans Matlab puisque ce sont elles qui constituent un de ses principaux atouts. Ces fonctions sont utilisables à partir d’un script ou directement de l’espace de travail.
3.3.2 Définition
Une fonction est définie par :
- son nom ;
- ses entrées ; - ses sorties. syntaxe générale : function [sortie_1,sortie_2,]=nom_fonc(entrée_1,entrée_2,)
3.3.3 Exemple de fonction
Pour illustrer le principe de construction d'une fonction, reprenons l’exemple du calcul des diagonales, mais en créant une fonction utilisable pour une matrice A quelconque. On exploiter cette fonction sous le prompt de Matlab.
3.4Structures de programmation usuelles
On rappelle dans ce paragraphe les principales structures de programmation que l’on rencontre en général. Sous Matlab, le nombre de ces structures est très réduit puisque l’on en a deux types :
for( k = Val_Init : Pas : Val_fin) while (condition)
endend
3.4.1 Structure de type test
if (condition) if (condition1)
elseelseif (condition2)
endelse
end
switch
case
otherwise
end
Remarque :
Comme Matlab est un logiciel interprété, il faut utiliser avec parcimonie les boucles for et while. Il vaut mieux dès que possible utiliser la boucle interprétée " : ".
Pour remplir un vecteur A des valeurs de 11 à 20, au lieu de :
A=zeros(1,10); for ii=1:10 A(ii)=ii+10; end
il vaut mieux
A=11:20;
ou bien
A=[1:10]+10;
Application :
A partir d’une matrice A et d’un vecteur vect, on veut calculer la matrice D telle que :
Figure n°9 : exemple d’utilisation des boucles et leurs inconvénients
3.5Bilan et Exercices d’application : Création d'une fonction
1) Générer un vecteur complexe défini par A=[ 0.22+0.5*i ; 0.4-0.2*i]
2) Extraire les parties réelles, imaginaires, modules et phases des éléments du vecteur A.
3) Créer une fonction farg_A permettant de calculer la phase des éléments complexes d'une matrice A. Deux arguments en entrée pour la fonction sont imposés: le premier représente la matrice A et le second est une variable texte qui permet de sortir le résultat, soit en radian, soit en degré. Strcmp
PARTIE N° 4GRAPHISME
4.1 Préambule
Une des priorités des « développeurs » de Matlab est aujourd’hui d’offrir aux utilisateurs un maximum d’outils graphiques. L’approche "orientée objet" a permis de donner une très grande efficacité et souplesse à ces outils. L’aspect des graphes que l’on manipule peut ainsi à tout moment être modifié par exemple par un changement de format du graphe, des couleurs ou du style de la représentation.
4.2 Notion de figure
Avant de détailler les différentes fonctions de visualisation, il faut noter que l’on peut générer simultanément plusieurs graphes à l’écran. Pour cela, on utilise la commande figure qui permet d’ouvrir autant de fenêtres graphiques que désiré. Chaque figure porte un numéro qui permet de la référencer et ainsi de savoir où l’on envoie les sorties graphiques. Les figures sont indexées automatiquement, la commande close permet de les fermer à partir de l’espace de travail. Il est à noter que toutes les fenêtres se ferment à l’aide de la commande close all.
Application :
Figure n°10 : ouverture et fermeture de fenêtre pour figure
4.3 Affichage des courbes 2D
Matlab possède un grand nombre de fonctions permettant de produire des courbes 2D. Chacune accepte en entrée des formes vectorielles ou matricielles automatiquement mises à l’échelle suivant les axes définis par ces données.
| Fonctions élémentaires | définition |
| plot | Affichage linéaire |
| loglog | Echelle log-log |
| semilogx | Echelle semilog sur x |
| semilogy | Echelle semilog sur y |
| line | Définition d’une ligne |
| Outils | définition |
| polar | Affi. en coordonnées polaires |
| bar | Affi. en mode escalier |
| hist | Affi. d’un histogramme |
| fplot | Affi. d’une fonction donnée |
| Outils | définition  |
| title | Création d’un titre |
| xlabel | Commentaire sur x |
| ylabel | Commentaire sur y |
| grid | Création d’une grille |
| text | Commentaire sur graphe |
| axis | Gestion des axes (zoom) |
| subplot | Multi-graphe sur même figure |
| hold | Mode surimpression |
4.3.1 Commande plot
La commande plot génère l’affichage des éléments d’un vecteur ou des colonnes d’une matrice. Si y est un vecteur, plot(y) produit un affichage linéaire des éléments de y suivant l’index du vecteur. Si on spécifie deux vecteurs en entrée plot(x,y), on obtient l’affichage des éléments de y suivant ceux de x. Les couleurs et les symboles associés aux données sont paramétrables (voir help plot).
Application :
1. Réaliser l’affichage de la fonction Chirp définie par sin(t2 )sur l’intervalle:0 < t < 5 avec un pas de 0.1 en utilisant la commande plot. Ajoutez une légende à l'aide de title, xlabel et ylabel.
2. Modifier le style de la courbe pour ne représenter que les points calculés, sans les lignes entre points consécutifs. Choisir ensuite votre propre mode de représentation.
4.3.2 Commande fplot
Cette commande permet d'afficher une fonction sans l'effet de l'échantillonnage. Pour cela, on doit en premier lieu créer une fonction Matlab représentant la fonction mathématique à étudier.
function x=chirp(t);
% Cette fonction crée un signal “chirp” x=sin(t.^2);
Puis, sous le prompt Matlab, on entre:
» fplot('chirp',[0 5])
Cette fonction calcule plus finement la fonction sur les portions où la fonction présente des discontinuités graphiques.
4.3.3 Commande subplot
Cette commande est un outil qui permet de gérer le nombre de graphes que l’on crée sur une même figure. Elle partitionne la figure comme une matrice (n,p) dont les éléments sont des graphes.
subplot(n,p,r)
où: n est le nombre de lignes, p est le nombre de colonnes, r est le numéro de placement dans la matrice (colonne par colonne).
|
|
|
|
Figure n°11 : utilisation du subplot
4.3.4 Commande axis
Lorsque l’on veut ne visualiser qu'une portion d'un vecteur de données, on utilise la commande axis. Elle peut être utilisée de la façon suivante :
2D axis([ xmin xmax ymin ymax])
3D axis([ xmin xmax ymin ymax zmin zmax])
Elle permet de gérer les échelles sur les différents axes. Elle peut en outre être utilisée comme un zoom statique. Il est à noter que cette commande permet aussi de gérer l'aspect général des axes. En effet, on peut l'utiliser avec du texte comme entrée, ainsi:
axis('square') l'espace graphique prend une forme carré. axis('equal') indique que les marqueurs sur les axes seront les mêmes. axis('off') supprime les axes à l'écran. axis('on') restaure les axes à l'écran.
4.4Affichage des courbes 3D
Comme pour le cas 2D, on dispose d'un certain nombre de fonctions de visualisation des données définies dans un domaine tridimensionnel.
| Visualisation 2D des données 3D | définition |
| contour | Courbes de niveaux |
| image | Visualisation par niveau de gris |
| imagesc | Idem mais non normalisé |
| mesh | Déformation d'une grille 3D. |
| meshc | Combinaison de mesh et de contour. |
| meshz | Combinaison de mesh plus projection sur le plan z=0. |
| surf | Idem que mesh, mais avec surface colorée. |
| plot3 | Visualisation de type plot, mais avec 3 vecteurs |
| Outils | définition  |
| colormap | Changement de palette de couleurs |
| view | Orientation de la vue 3D |
| meshgrid | Définition des matrices représentant la grille |
Certaines de ces fonctions attendent des arguments de type vectoriel ou matriciel.
4.4.1 plot3 : arguments vectoriels
Cette fonction est identique à la commande plot, mais avec x, y et z comme arguments. Application : Définir une variable définissant le segment [0,10?] par pas de ?/50. Entrer la commande plot3(sin(t),cos(t),t)
4.4.2 Fonctions à arguments matriciels
Ces fonctions permettent de visualiser des données définies sur une grille représentée par une matrice. Différentes possibilités de visualisation existent :
- soit par niveau de gris (0-256) -->> image
- soit par niveau d'amplitude -->> contour
4.4.3 meshgrid
Toutes ces fonctions nécessitent des matrices comme entrées. Dans certains cas, on est obligé de générer soi-même la matrice à visualiser. Pour cela, Matlab possède une fonction qui permet d'obtenir les points de la grille représentant les x et y.
Application :z x y( , ) = ?3 1( x)2 e? ? +x2 (y 1)2 ?10( x ? ?x 3 y 3 )e? ?x2 y2 ? 1e? + ?(x 1)2 y2
5 3
On choisit pour cela la région:
??3 ? x ? 3
?
??3 ? ?y 3
Pour définir la grille de visualisation à partir des vecteurs définis plus haut, on utilise la commande meshgrid :
[X,Y]=meshgrid(-3:1/8:3);
La matrice Z contient tous les points calculés à partir de la grille générée par les matrices X et Y.
| ?x( )1 ? ?x( )2 ?x( )3 | x( )1 x( )2 x( )3 | x( )1 x( )2 x( )3 | x( )1 x( )2 x( )3 | x( )1 x( )2 x( )3 | x( )1 x( )2 x( )3 | ? ?y( )1 ? ?y( )1 ? ? ? ?y( )1 = | y( )2 y( )2 y( )2 | y( )3 y( )3 y( )3 | y( )4 y( )4 y( )4 | y( )5 y( )5 y( )5 | y( )6 y( )6 y( )6 | ? ? ? ? |
| x(4)x( )4 |
| y(3)y( )3 |
X =?x( )4 x( )4 x( )4 x( )4 x( )4 ?Y?y( )1 y( )2 y( )4 y( )5 y( )6 ?
?? ??
| ?x( )5 ?? | x( )5 | x( )5 | x( )5 | x( )5 | x( )5  | ? ?? | ?y( )1 ?? | y( )2 | y( )3 | y( )4 | y( )5 | y( )6 | ? ?? |
Il suffit alors d'utiliser l'opérateur "élément par élément" pour les opérations sur les matrices ainsi définies. Le début du programme s'écrit donc :
% Visualisation 3D [x,y]=meshgrid(-3:1/8:3); z = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) - 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) - 1/3*exp(-(x+1).^2 - y.^2);
On étudie maintenant les différents outils pour visualiser la matrice Z.
4.4.4 plot
Cette fonction, la plus simple, permet de tracer une ligne pour chaque colonne de la matrice Z.
4.4.5contour et contour3
Avec la fonction contour, on visualise les données contenues dans la matrice Z par courbes de niveau. Matlab trace les courbes joignant les mêmes niveaux d'amplitude de la matrice Z sur un plan 2D. Contour3 réalise la même fonction, mais dans un plan 3D, le nombre de niveaux étant paramétrable.
contour(x,y,z,M)
où x, y sont les matrices ou vecteurs des axes, z la matrice des amplitudes et M le nombre de niveaux. Exemple :
figure(1); contour(Z,20) figure(2); contour3(Z,20)
4.4.6 mesh et surf
Les commandes mesh et surf affichent une surface en 3 dimensions en perspective. La commande mesh associe les couleurs aux éléments de la grille tandis que surf colore les facettes de la grille. (idem pour surfc, meshc, meshz) mesh(x,y,z,C) ; surf(x,y,z,C)
où x, y sont les matrices ou vecteurs des axes, z la matrice des amplitudes et C représente le mode d’évolution de la couleur.
Figure n°13 : fonctions à argument matriciel
4.4.7image
| fonctions | définition |
| image | Affichage d’une image |
| imagesc | Affichage d’une image avec son intensité |
| imread | Lecture d’un fichier image à un format donné |
| imwrite | Ecriture d’un fichier image à un format donné |
| iminfo | lecture des informations d’un fichier image |
La commande image restitue la matrice d'entrée sous forme d'une carte 2D avec des niveaux de gris correspondants. La matrice d'entrée doit donc être normalisée par rapport aux m niveaux de couleurs de la carte sélectionnée. En réalité, cette fonction est un cas particulier de la commande pcolor qui peut être totalement paramétrable dans la définition de ces axes, la gestion des couleurs, etc.
Si on désire utiliser une matrice non normalisée par rapport à la palette de couleurs, il faut travailler avec la commande imagesc.
4.4.8colormap et colorbar
La fonction colormap permet de sélectionner une palette de couleurs prédéfinie. Une palette de couleurs est un tableau de taille (m,3) dont les lignes spécifient l'intensité en code RGB (Red, Green, Blue) de la façon suivante:
map k( ,:) = [r k( ) g k( ) b k( )] avec 0 ? r(k), g(k),b(k) ? 1
Exemple de codes :
| [0 0 0] | noir |
| [1 1 1] | blanc |
| [1 0 0] | rouge |
| [.5 1 .83] | bleu marine |
Par défaut, m vaut 64. Il peut aller jusqu'à la valeur 256. Matlab propose plusieurs palettes de couleurs: hsv, hot, cool, jt, pink, copper, gray.
Pour associer les couleurs aux données, Matlab segmente l'axe des z, en utilisant [zmin,zmax], en un nombre d'intervalles correspondant aux nombres de lignes de la palette de couleurs. Pour visualiser la palette avec les segments, on peut utiliser la commande colorbar.
4.4.9 view
Lorsque l'on utilise une commande de visualisation 3D, la courbe apparaît sous un angle de vue donné. Grâce à la commande view, on peut faire varier les angles de point de vue. Le repère utilisé est le suivant:
view([xe ye ze])
Par défaut, les arguments ont comme valeurs (0,90) pour des graphiques 2D et (-37.5,30) pour des graphiques 3D.
Matlab permet aussi de générer des graphiques de très haute qualité avec des effets d'éclairage, de texture etc. La commande shading offre la possibilité de faire disparaître la grille et interp permet de réaliser une interpolation afin de créer un effet de texture. La commande light permet de gérer la position d’éclairage de la figure. La commande material offre la possibilité de modifier le type de reflet de la courbe.
Exemple : un effet d'éclairage
4.5Graphes spécialisés
4.5.1 Barres et surfaces
| fonctions | définition  |
| bar | Barres verticales |
| barh | Barres horizontales |
| bar3 | Barres verticales 3d |
| bar3h | Barres horizontales 3d |
| area | Surfaces |
Exemple :
Figure n°14 : exemple d’utilisation de graphes spécialisés
4.5.2 Camemberts
| fonctions | définition |
| pie | Camembert |
| pie3 | Camembert 3d |
Exemple :
Figure n°15 : autre exemple d’utilisation de graphes spécialisés
4.6Exercice : graphisme et fonctions
On propose de réaliser l'étude du polynôme suivant :
p x( ) = ?x3 30x + 30
1) Evaluer le polynôme sur le segment [-8,8] pour un pas de calcul de 0.1. polyval
2) Visualiser la courbe ainsi définie (Utiliser la notion de boucle interprétée). plot,grid
3) Calculer les racines et les afficher sur le même graphique que précédemment. roots, hold, zeros, length
4) Créer une fonction mypoly.m représentant le calcul du polynôme pour un x donné. 5) Evaluer l'aire formée par la courbe entre les deux premières racines.
quad
6) Visualiser graphiquement l'aire calculée
fill
4.7Autre exercice
On se propose d’identifier le polynôme d’ordre n qui va modéliser la courbe suivante :
y(x) = sin(x) + sin(3.2x) pour x?[0,?]
Générer un jeu de données avec un pas=pi/256.
A l’aide de commande polyfit, calculer les coefficients du polynôme qui modélise la fonction y(x) au sens des moindres carrés. Calculer à l’aide de polyval la courbe obtenue et visualiser la ainsi que y(x).
Calculer la norme de l’erreur de modélisation pour toutes les valeurs de l’ordre comprises entre 1 et 10. Visualiser la courbe obtenue.
E(x) = y(x) ? p(x) avec p x( ) = a x1n + a x2n?1 + + a xn1 + an+1
4.8Exercice images
La manipulation et l'affichage des images est pris en charge par l'Image Processing Toolbox sous Matlab. Une description assez complète peut être visualisée en tapant "doc images". Le but de cet exercice est d'afficher une image chargée depuis un fichier, et de lui superposer un graphique vectoriel dépendant du clic de l'utilisateur.
1) Chargez l'image '' en mémoire (imread), et affichez la (imshow). Testez les outils de visualisation d'une image (zoom, curseur…).
2) Définissez une courbe paramétrisée par t qui échantillonne un cercle de rayon r=20 centré en (x0,y0) arbitraire, selon les équations suivantes:
x = x0 + cos(t) * r y = y0 + sin(t) * r
Evaluez cette courbe pour t allant de 0 à 2*pi par pas de pi/10, et affichez la (plot).
3) Récupérez la position [x0,y0] d'un clic de souris sur l'image (ginput), afin de définir un cercle centré sur cette position.
A l'aide de holdon, affichez l'image, puis superposez le cercle à l'image.
PARTIE N° 5FICHIERS DE DONNEES
Matlab possède deux types de fichiers. Le premier type est constitué par les fichiers créés à un format propriétaire à Matlab. Ces fichiers sont reconnaissables par leur extension en .mat. Ce format spécifique permet de sauvegarder des variables au format numérique ou texte, des variables réelles ou complexes très simplement. Le second type regroupe les fichiers binaires et ASCII communs à tous les langages de programmation. Ces derniers permettent donc de communiquer avec l'extérieur et en particulier de rapatrier des données collectées par d'autres logiciels.
5.1Fichiers Matlab
Les fichiers nom_fic.mat constituent donc le système de fichiers propres à Matlab. Leur manipulation est très facile, quel que soit le type ou la taille des matrices que l'on désire sauvegarder.
5.1.1 Commande save
Cette commande permet de créer ce premier type de fichier. La syntaxe est la suivante : savenom_fich var1 var2
Les variables sont sauvegardées comme des matrices et donc se retrouvent au même format lorsqu’on les recharge afin de réutiliser.
Remarque: on peut sauvegarder une matrice var au format ASCII (8 ou 16 bits) savePATH/nom_fich var -ascii
5.1.2 Commande load
Cette commande permet la relecture des variables sauvegardées avec la commande save.
loadPATH/nom_fich
Remarque: La commande load offre aussi la lecture de fichier ASCII sous forme d'une matrice var
var = load
5.2Fichiers binaires et ASCII: le format standard
Ce type de fichier permet d'importer et d'exporter des données vers l'extérieur dans le format de son choix. Les commandes nécessaires à leur manipulation sont les suivantes :

| fopen | fseek | sprintf |
| fread | ferror | fscanf |
| fwrite | ftell | sscanf |
| fclose | fpr | intf |
5.2.1 Commande fopen
Cette commande ouvre et donne des informations sur le fichier que l'on désire manipuler. Il y a deux types de syntaxes :
fid = fopen('filename')
fid = fopen('filename','permission')
[fid,message] = fopen('filename','permission','architecture')
[filename,permission,architecture] = fopen(fid)
Ces trois premières commandes correspondent toutes à l'ouverture d'un fichier dans le mode spécifié par l'argument permission.
| r: | Ouverture en lecture. |
| r+: | Ouverture en lecture et en écriture. |
| w: | Efface le contenu ou crée un nouveau fichier et le place en mode écriture. |
| w+: | Efface le contenu ou crée un nouveau fichier et le place en mode écriture/lecture. |
| a: | Crée un nouveau fichier ou ouvre un fichier existant pour l'écriture à la suite des |
| données déjà présentes. | |
| a+: | idem mais en lecture/écriture. |
Si la commande a réussi, la variable fid devient un entier > 2 et la variable message est vide.
Si la commande n'a pas réussi, la variable fid prend la valeur -1. Dans ce cas, un texte a été associé à la variable message qui peut vous aider à définir l'erreur de manipulation.
5.2.2Commande fread
Elle permet la lecture d'un fichier de données binaires. Sa syntaxe est la suivante:
[A,count] = fread (fid,size,'precision')
La commande freadpermet donc la lecture d'un fichier binaire spécifié par fid et écrit les données dans une matrice A. fread réalise la lecture d'un nombre d'éléments spécifié par size suivant une précision donnée.
Si l'argument size est donné, les entrées possibles sont: n : lit n éléments vers un vecteur colonne.
inf : lit toutes les données et crée un vecteur de même taille (par défaut). [m,n] lit (m*n) éléments et crée une matrice de taille [m,n] suivant l'ordre des colonnes. Si la taille du fichier est inférieure, le reste se trouve combler par des zéros.
L'argument précision correspond à la précision numérique utilisée pour sauvegarder les données. Il correspond au nombre d'octets alloué à la variable pour coder sa valeur. Un standard de précision indépendant de la machine source est le float32 et float64. Ce format permet une bonne portabilité.
Matlab Langage C et Fortran
| 'schar' | 'signed char' | Signed character; 8 bits |
| 'uchar' | 'unsigned char' | Unsigned character; 8 bits |
| 'int8' | 'integer*1' | Integer; 8 bits |
| 'int16' | 'integer*2' | Integer; 16 bits |
| 'int32' | 'integer*4' | Integer; 32 bits |
| 'int64' | 'integer*8' | Integer; 64 bits |
| 'uint8'  | 'integer*1' | Unsigned integer; 8 bits |
| 'uint16' | 'integer*2' | Unsigned integer; 16 bits |
| 'uint32' | 'integer*4' | Unsigned integer; 32 bits |
| 'uint64' | 'integer*8 | Unsigned integer; 64 bits |
| 'float32' | 'real*4' | Floating-point; 32 bits |
| 'float64' | 'real*8' | Floating-point; 64 bits |
| 'double' | 'real*8' | Floating-point; 64 bits |
| formats portables | ||
| 'char' 'char*1' | Character; 8 bits | |
| 'short' 'short' | Integer; 16 bits | |
| 'int' 'int' | Integer; 32 bits | |
| 'long' 'long' | Integer; 32 or 64 bits | |
| 'ushort' 'unsigned short' | Unsigned integer; 16 bits | |
| 'uint' 'unsigned int' | Unsigned integer; 32 bits | |
| 'ulong' 'unsigned long' | Unsigned integer; 32 or 64 bits | |
| 'float' 'float' | Floating-point; 32 bits | |
5.2.3 Commande fwrite
fwrite permet l'écriture de données contenues dans une matrice. Sa syntaxe est la suivante: count = fwrite(fid,A,'precision')
Elle permet donc de passer des données contenues dans la matrice A (sauvegarde dans le sens des colonnes) vers un fichier défini par fid suivant une précision donnée. Count correspond au nombre de données effectivement translatées.
5.2.4 Commande fclose
Cette commande correspond à la fermeture d'un ou de plusieurs fichiers. Sa syntaxe est:
status = fclose(fid) status = fclose('all')
5.2.5 Commande fprintf
Cette commande est l'analogue de la commande fprintf en C: elle permet d'écrire une chaîne de caractère ASCII dans le fichier. Cette chaîne de caractères peut contenir des caractères de formatage, qui seront alors remplacés par les données numériques passées en argument. Par exemple, la commande suivante écrira "x=2" dans le fichier associé à fid:
x=2;
fprintf(fid, 'x=%d', x);
5.3Exercice
1) Définissez une matrice A:
Effacez l'ensemble des variables (clear all)
Chargez le fichier (load)
Vérifiez que la matrice A a bien été lue à partir du fichier.
2) Même question en enregistrant la matrice dans un fichier '' au format ASCII à l'aide de save et load.
Vérifiez à l'aide du bloc note que le fichier contient bien les valeurs de la matrice A de façon lisible.
3) Même question en enregistrant la matrice dans un fichier '' au format binaire, en utilisant fopen, fwrite, fread et fclose. On utilisera par exemple une précision 'double'.
La fonction fread ne renvoie pas une matrice, mais un vecteur; pourquoi ?
Quelle fonction matlab utiliser pour redonner sa "forme" 4x3 à la matrice ?
PARTIE N° 6APPLICATIONS
6.1Rappels sur le développement en série de Fourier et Transformée de Fourier
Tout signal v(t) périodique et de période T peut se décomposer en série de Fourier. Ainsi, en prenant
? 2k? ?

ak vs ( )t cos? t?dt
T ? T ?
k 2 T / 2 ( ) ? 2k? ?
b = ? T / 2 vs t sin? t?dt
T? ? T ?
la décomposition en séries de Fourier de v(t) est alors
v( )t = a0 +?? ak cos?? 2k?t??+bk sin?? 2k?t??.
2 k=1 ? T ? ? T ?
Une autre écriture est souvent utilisée, surtout en traitement du signal : il s’agit du développement en série de Fourier en termes complexes.
( ) ? ? 2? ? v t = ? ck exp? jk t?
k=?? ? T ?
avec ck = 1 vs ( )t exp??? jk2?t??dt .
T? T ?
Les coefficients ck et c?k sont complexes conjugués et sont liés aux quantités ak et bk comme suit :
ck =(ak ? jbk ) et c?k =(ak + jbk )
?
Il est à noter que ck = c?k et que ck = ck exp(j?k ) avec ?k =?Arctan?? bk ??? .
? ak ?
On peut aussi exprimer le signal v(t) à partir de ?k . On a
?
v( )t = c0 +?2ck cos?? 2k?t +?k ?? . k=1 ? T ?
Remarque : Le signal périodique n’est pas à énergie finie sur l’intervalle ]?? ; +? [.
Cela revient à dire que la quantité
dt
| n’a pas une valeur finie. v(t) n’est donc pas de carré intégrable. | |
| Remarque 2 : | On constate en outre que d’après l’égalité de Parseval, |
| ? 2 ? ck = 1 ? v( )t 2dt k=1 TT ? 2 Si v(t) est réel, ck=1 ?v2 ( )t dt . La puissance moyenne totale du k=1 TT signal est donc égale à la somme des puissances moyennes des différents harmoniques et de la composante continue. | |
| Remarque 3 : | On rappelle que la valeur moyenne d’un signal périodique est donnée par |
| µ= 1 ?0T v( )t dt . T |
Figure n°16 : spectre d’amplitude du signal périodique
Le spectre du signal périodique v(t) a une représentation spectrale discrète.
6.2Exercice
6.2.1Décomposition en série de Fourier, représentation spectrale et somme de série Soit y(t) la fonction de période 2? définie sur [??;?] par :
y( )t =?? 0 si ??? t ? 0 ?sin( )t si 0 ? t ??
Développer cette fonction en série de Fourier à partir des fonctions sinus et cosinus ;
Représenter la somme du fondamental avec les 5, puis 10 puis 30 premiers harmoniques. On créera pour cela une fonction.
Vérifier la formule . On utilisera Matlab pour visualiser l’évolution de la
p=1 4p ?1 2
fonction g( ) .
p=1 4p ?1
