Correction des exercices sur la finance de marche : theorie moderne du portefeuille et correction

Correction des exercices sur la finance de marché : théorie moderne du portefeuille et correction
1 Introduction
Le but de cette correction d’examen "type" est de couvrir l’ensemble du programme de finance de marché (gestion de portefeuille) d’un master en rappelant bien les bases théoriques afin de pouvoir être lue sans autre support (pour approfondir la théorie, vous pouvez consulter les deux ouvrages de référence section.
2 Espérance, Ecart-type, Skewness et Kurtosis
L’espérance mesure le rendement annuel moyen que l’on peut attendre d’un placement :
E(X )Ƨpi xi
L’écart-type est la racine carrée de la variance (exprimable en pourcentage donc) :
qq¾iÆ §pi (xi ¡E(X ))2 Æ [§pixi2 ¡E(X )2
La volatilité annualisée est une mesure du risque annualisée :
…
Skewness ou coefficient d’asymétrie : c’est un moment d’ordre 3, il est nul si et seulement si la loiest symétrique par rapport à la moyenne. Un investisseur prudent préférera une skewness positive.
Kurtosis ou coefficient d’aplatissement est un moment d’ordre 4, il renseigne sur les réalisationsde valeurs extrêmes (ce qu’on appelle queues de distribution, ce sont les risques extrêmes). Un K È 3 indique des queues de distribution plus épaisses que celles de la loi normale, ce que n’aimera donc pas un investisseur averse au risque. Pour une loi normale, K Æ 3.
Résultats numériques :
|
Fond A |
Fond B |
Fond C |
|
|
E(R) |
11,30% |
8,08% |
6,98% |
|
V |
0,0053 |
0,0036 |
0,0064 |
|
¾ |
7,25% |
5,98% |
8,00% |
|
S |
-2,29 |
-0,25 |
-0,55 |
|
K |
8,35 |
1,81 |
3,32 |
Intuition concernant la normalité des portefeuilles : C a une skewness et kurtosis proche de la loi normale. On note que le portefeuille A a une survenance d’évènements extrêmes plus grande que celle d’une loi normale.
3 Normalité de la distribution des rendements
Le test de Jarque-Bera est un test d’hypothèse qui cherche à déterminer si des données suivent une
« loi normale ». On teste :
— H0 : les données suivent une « loi normale » (S Æ 0 et K Æ 3), contre
— H1 : les données ne suivent pas une « loi normale » (S 6Æ0 et K 6Æ3). La statistique de test est :
J BÆ n¡6k (S2Å(K ¡43)2)
Avec :
— n = Nombre d’observations
— k = Nombre de variables explicatives si les données proviennent des résidus d’une régression linéaire. Sinon, k=0.
— S = Skewness
— K = Kurtosis
La statistique JB suit asymptotiquement un Â2 à 2 degrés de liberté. La p-value (ou probabilité cri-tique) mesure le risque de rejeter à tort H0 (on rejette H0 si p ¡v al ue Ç (1 ¡®) Æ 5% typiquement), ® est le risque de première espèce en pourcentage, 95% en général.
Ici on a donc a ne pas rejeter l’hypothèse H0 pour le portefeuille C, on considère que les données mesurées pour C suivent une loi normale.
4 Semi-Variance
La semi-variance ou Downside-risk est une mesure du risque qui apporte l’avantage de ne prendre en compte que les variations en dessous d’un seuil de rendement, un investisseur appréciera en effet un saut de rendement tandis qu’il n’aimera pas une baisse de rendement.
5 Lower Partial Moments
Le Lower Partial Moment est la somme des déviations pondérées des rendements potentiels à par-tir d’un niveau plancher r¤, où chaque déviation est mise à la puissance n.
Comme la semi-variance, le Lower Partial Moment est une mesure asymétrique du risque.
Le paramètre n peut être considéré comme une mesure de l’aversion du risque de l’investisseur. Plus on est averse à la perte (shortfall) plus n sera grand.
|
r ¤ |
K |
|
LP MnÆ |
pp(r ¤¡Rp)nÆ pp[mi n(0,Rp¡r ¤)]n |
|
X |
X |
|
Rpơ1 |
pÆ1 |
Pour r¤ Æ E(X ) et n Æ 2, on retrouve un Lower Partial Moment qui s’apparente à la semi-variance.
6 Value at Risk
La Value at Risk (VaR) est l’estimation de la perte maximale possible pour un seuil de sûreté prédé-fini sur une période de temps donnée.
Pr ob(Rp· V aR®)Æ1¡®
Exemple : 1-day 99% le seuil de sûreté est 100 "
— 99 % de chance de perdre moins de 100 " en 24 heures
— ou 1 % de chance de perdre plus de 100 " en un jour
Parametric VaR
- on suppose que les rendements suivent une loi (ici on prendra la loi normale)
- on calcule la moyenne ¹ Æ E(X ) et l’écart-type ¾
- on utilise le 95ème percentile de la loi normale : 1,65 (ou 2,33 pour 99%)
Ici : V aR95% Æ E(X ) ¡1, 65¾
Résultats numériques :
|
Fond A |
Fond B |
Fond C |
|
|
VaR 95% |
-0,67% |
-1,79% |
-6,22% |
VaR historique
- distribution d’un an de rendement du stock
- simuler le rendement du placement actuel
- ordonner les résultats obtenus
- on considère qu’il y a 252 jours ouvrés par an, on prend la moyenne des 2 plus mauvais pour la VaR 99% ou la moyenne des 12 pires pour laVaR 95%
Ici, on observe le tableau et on obtient :
|
Fond A |
Fond B |
Fond C |
|
|
VaR 95% |
-5% |
-4% |
-4% |
Méthodes d’estimation de la VaR :
— paramétrique : on suppose que les rendements suivent une densité de probabilité définie (e.g. normale, t-Student, etc.) et la mesure de risque est déduite des quantiles de la loi retenue ;
— non paramétrique : les calculs sont alors effectués sur les données observées (exemple de la VaR historique : on estime empiriquement la distribution des pertes et leurs fréquences d’ap-parition en fixant un niveau de probabilité voulu) ;
— semi-paramétrique : c’est un mélange des deux méthodes précédentes où l’on ajuste la volati-lité estimée par moyenne mobile exponentielle sur données historiques, ou en effectuant une expansion de Cornish-Fisher et autres méthodes à régression sur quantiles.
…
Limite VaR
La VaR ne respecte pas le critère de sous additivité : celle-ci implique que le risque agrégé d’un portefeuille ne puisse être supérieur à la somme des risques de ses composantes (½(X ÅY ) · ½(X ) Å ½(Y )).
La VaR n’apporte aucune information sur la taille des pertes une fois la VaR franchie. Pour remédier à ces deux problèmes, on introduit l’expected shortfall (ES).
L’Expected Shortfall est la moyenne des rendements une fois la VaR franchie, ce sur une période donnée. Elle est aussi appelée C-VaR ou Tail-Loss :
E S(®)Æ E[r jr Ç V aR(®)]
7 Analyses de styles de portefeuilles
Analysis - Return based
Avantages :
— caractérise l’ensemble du portefeuille
— comparaison facile entre les portefeuilles
— agrège les effets des investissements
— rapide et peu coûteuse à réaliser Désavantages :
— peut ne pas caractériser le style actuel du portefeuille
— sensible à la définition du style de portefeuille
— biaisée par la multicolinéarité de différents styles
versus
Analysis - Holding based
Avantages :
— caractérise chaque position
— comparaison en les positions individuelles aisées
— prise en compte rapide des changements de style Désavantages
— sensible aux attributs de classification des styles
— plus insensible aux données que le return-based style analysis
Styles
— small versus lager (taille de la capitalisation)
— value versus growth (ratio book to market, high versus low, croissance du chiffre d’affaire)
Critère moyenne variance Pour une espérance de rendement donnée, on choisit l’actif qui a laplus faible variation de rendement :
|
Fond A |
Fond B |
Fond C |
|
|
E(R) |
11,30% |
8,08% |
6,98% |
|
V |
0,0053 |
0,0036 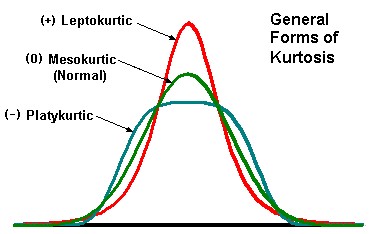 |
0,0064 |
E(A)È E(B) V (A)È V (B) : MV indéterminé entre A et B
E(A)È E(C ) V (A)Ç V (C ) : MV on préfère A à C
E(B)È E(C ) V (B)Ç V (C ) : MV on préfère B à C
Critère de la dominance stochastique d’ordre 1 Une variable aléatoire x domine une variable aléa-toire y au sens de la dominance stochastique d’ordre 1 lorsqu’elle est préférée à la seconde par tous les individus dont la fonction d’utilité croit avec la richesse.
Théorème DS1 : Si l’on note F et G les fonctions de répartition des variables aléatoires x et y, la variable x domine la variable y au sens de la dominance stochastique d’ordre 1 si et seulement si F (z)· G(z) avec a · z · b. L’intervalle [a,b] représente le domaine de variation des aléas.
Remarque : le graph de la fonction de répartition de la variable "dominante" x sera à la droite de celui de la variable y dominée.
Remarque : lorsqu’on se trouve dans une situation où les fonctions de répartition sont sécantes, on ne peut plus classer les variables aléatoires correspondantes selon ce critère de DS1, on introduit alors l’aversion au risque et la dominance stochastique d’ordre 2.
|
Rdts |
Fond A |
Fond B |
Fond C |
F(A) |
F(B) |
F(C) |
F(A)-F(B) |
F(A)-F(C) |
F(B)-F(C) |
|
-0,20 |
0,02 |
0,02 |
0,02 |
0,02 |
0,02 |
-0,02 |
|||
|
-0,05 |
0,03 |
0,02 |
0,05 |
0,02 |
0,02 |
0,03 |
0,03 |
||
|
-0,04 |
0,03 |
0,03 |
0,05 |
0,05 |
0,05 |
||||
|
0,00 |
0,15 |
0,05 |
0,05 |
0,2 |
-0,15 |
-0,15 |
|||
|
0,01 |
0,15 |
0,15 |
0,2 |
0,2 |
0,2 |
||||
|
0,02 |
0,35 |
0,2 |
0,2 |
0,55 |
-0,35 |
-0,35 |
|||
|
0,05 |
0,35 |
0,2 |
0,55 |
0,55 |
-0,35 |
-0,35 |
|||
|
0,14 |
0,35 |
0,4 |
0,55 |
0,95 |
0,55 |
-0,4 |
0,4 |
||
|
0,15 |
0,4 |
0,4 |
0,95 |
0,95 |
0,95 |
||||
|
0,16 |
0,05 |
0,05 |
0,05 |
1 |
1 |
1 |
Selon le critère de la DS1, tout est indéterminé.
Pour le cas gaussien, le critère moyenne variance implique que A est préféré à C et B à C pour la DS1.
Critère de la dominance stochastique d’ordre 2 On dit d’une variable aléatoire x qu’elle domineune variable aléatoire y au sens de la dominance stochastique de deuxième ordre lorsqu’elle est préférée à la seconde par tous les individus dont la fonction d’utilité est monotone, croissante et concave. On aura alors :
E(U (x))¸ E(U (y))
Avec U(.) appartenant à la classe des fonctions d’utilité monotones croissantes et concaves. La dominance est stricte si l’inégalité est stricte pour au moins une fonction d’utilité.
Ainsi, si F et G sont les fonctions de répartition de deux VA x et y, la variable x domine la variable y au sens de la dominance stochastique d’ordre deux si et seulement si :
Z t (F (z) ¡G(z))d z · 0 8t²[a,b] a
L’intervalle [a,b] représente le domaine de variation des aléas. La dominance est stricte dès lors que l’inégalité est stricte pour au moins une valeur de t.
Remarque : Cette inégalité signifie donc que la surface délimitée par le graph’ de la fonction de ré-partition de l’aléa x est en tout point t inférieure ou égale à celle délimitée par le graph’ de la fonction de répartition de y.
|
Rdts |
F(A) |
F(B) |
F(C) |
int(A) |
int(B) |
int(C) |
intA-intB |
intA-intC |
intB-intC |
|
-0,20 |
0,02 |
0,02 |
|||||||
|
-0,05 |
0,05 |
0,02 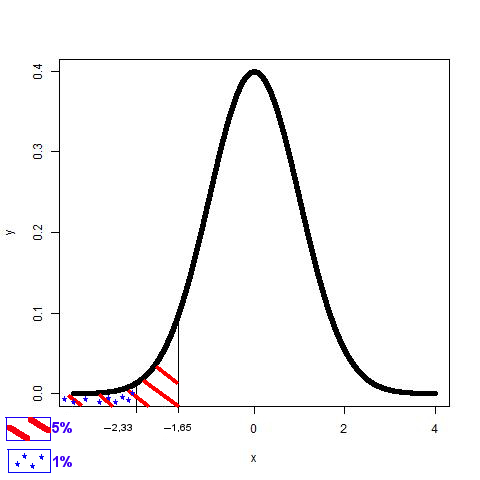 |
0,02 |
0,003 |
0,003 |
0,003 |
-0,003 |
||
|
-0,04 |
0,05 |
0,05 |
0,05 |
0,0035 |
0,0002 |
0,0032 |
0,0033 |
0,0003 |
-0,003 |
|
0,00 |
0,05 |
0,05 |
0,2 |
0,0055 |
0,0022 |
0,0052 |
0,0033 |
0,0003 |
-0,003 |
|
0,01 |
0,2 |
0,2 |
0,2 |
0,006 |
0,0027 |
0,0072 |
0,0033 |
-0,0012 |
-0,0045 |
|
0,02 |
0,2 |
0,2 |
0,55 |
0,008 |
0,0047 |
0,0092 |
0,0033 |
-0,0012 |
-0,0045 |
|
0,05 |
0,2 |
0,55 |
0,55 |
0,014 |
0,0107 |
0,0257 |
0,0033 |
-0,0117 |
-0,015 |
|
0,14 |
0,55 |
0,95 |
0,55 |
0,032 |
0,0602 |
0,0752 |
-0,0282 |
-0,0432 |
-0,015 |
|
0,15 |
0,95 |
0,95 |
0,95 |
0,0375 |
0,0697 |
0,0807 |
-0,0322 |
-0,0432 |
-0,011 |
|
0,16 |
1 |
1 |
1 |
0,047 |
0,0792 |
0,0902 |
-0,0322 |
-0,0432 |
-0,011 |
DS2 : indifférent entre A et B et entre A et C DS2 : préfère B à C
Pour le cas gaussien, le critère moyenne variance implique que A est préféré à C et B à C pour la DS2.
Critère de Roy avec un rendement minimum RL de -1%
Le critère de Roy sélectionne l’actif qui minimise le risque de ne pas atteindre un niveau de rende-ment minimum spécifié (MAR = minimum acceptable risk) :
Mi nPr ob(RpÇ RL)
Dans le cas de la distribution normale, le critère de Roy équivaut à :
|
Mi n Pr ob( |
Rp¡Rp |
Ç |
RL¡Rp |
) |
ou encore : M ax( |
Rp¡RL |
) |
||||||||
|
¾p |
¾p |
¾p |
|||||||||||||
|
L’application numérique donne : |
|||||||||||||||
|
E(RA)¡(¡1%) |
Æ 1, 7 |
E(RB)¡(¡1%) |
Æ 1, 52 |
E(RC)¡(¡1%) |
Æ |
1 |
|||||||||
|
¾A |
¾B |
¾B |
|||||||||||||
Dans le cas gaussien, on préférera A sur B sur C suivant le critère de Roy avec un rendement minimum de ¡1%
Dans le cas de la distribution anticipée par les analystes, on observe directement dans le tableau :
Pr ob(RAÇ ¡1%)Æ5% Pr ob(RBÇ ¡1%)Æ5% Pr ob(RCÇ ¡1%)Æ5%
Roy : indifférent entre A, B et C.
Critère de Kataoka avec une probabilité de 5%
Le critère de Kataoka choisit le portefeuille qui maximise la limite de rendement RL, sous la contrainte que la probabilité que le rendement du portefeuille soit inférieur à RL soit inférieure à la probabilité
Le critère s’écrit :
M ax(RL) sous contrainte Pr ob(RpÇ RL)· ®
Dans le cas gaussien, cela revient à :
…
D’où le cas gaussien pour Kataoka on préférera A sur B sur C car :
RLAÆ E(RA)¡1, 65¾(RA)Æ ¡0, 67%
RLBÆ E(RB)¡1, 65¾(RB)Æ ¡1, 79%
RLCÆ E(RC)¡1, 65¾(RC)Æ ¡6, 22%
Dans le cas de la distribution anticipée par les analystes, on observe le tableau pour
Pr ob(RiÇ RL)·5%
RLAÆ1% RLBÆ1% RLCÆ0%
pour le cas gaussien, on est indifférent entre A et B mais on les préfère à C.
Critère de Telser avec RL égal à -1% et une probabilité de 5%
Le critère de Telser choisit le portefeuille avec le meilleur rendement sous contrainte d’obéir à une contrainte de risque. C’est une combinaison de Roy et Kataoka. L’investisseur choisit deux données subjectives :
— choix du niveau de risque acceptable ®
— choix du rendement minimum acceptable RL
|
A |
B |
C |
|
|
E(R) |
11,30% |
8,08% |
6,98% |
|
Pr ob(RpÇ ¡1%)·5% |
ok |
ok |
ok |
Pour ce critère-là, on préférera A sur B sur C.
Pour le cas gaussien, A ne respecte pas le critère, et on préférera B à C.
Critère de la moyenne géométrique
On sélectionne le portefeuille avec la plus grande moyenne géométrique.
RGÆQ[1ÅRi]pr obi¡1i
|
Fond A |
Fond B |
Fond C |
||
|
RG |
11,04% |
7,91% |
6,67% |
|
|
Moyenne géométrique : A > B > C |
||||
9 Utilité de l’investisseur et caractérisation de son comportement
U 0(W )ÆW20¸0 et U 00(W )Æ¡W202·0
Fonction d’utilité croissante avec la richesse et individu averse au risque, c’est une fonction CRRA (constant relativ risk aversion).
|
u00 |
ARR= AAR£W |
u000 |
|
AAR=¡ u0 |
P Æ ¡u00 |
|
|
u0000 |
u00000 |
|
|
T Æ ¡u000 |
A Æ ¡u0000 |
L’indice d’aversion absolue pour le risque indique la façon dont la demande d’actifs risqués évolue avec la richesse de l’agent.
L’indice d’aversion relative pour le risque décrit la façon dont la proportion investie en actifs ris-qués évolue avec la richesse.
L’indice de prudence reflète l’aversion au risque de perte ou downside risk et la préférence pour l’asymétrie positive (Skewness È 0).
L’indice de tempérance va refléter le comportement d’un agent lorsque celui-ci fait face à un risque non assurable. Un agent qui présente de la tempérance et qui fait face à un risque de revenu non assurable réduira sa part d’actifs risqués dans son portefeuille (son exposition à d’autres risques) même si les risques sont statistiquement indépendants.
L’indice d’anxiété va refléter la réaction d’un agent face à des risques multiples.
…
Si l’investisseur est rationnel, il va maximiser son espérance d’utilité :
Max Esp(U)
U (W )Æ10Å20l n(W ) avec W Æ W0(1ÅRi )
…
Il choisit donc d’investir toute sa richesse dans A.
On considère un agent face à des loteries qui diffère par leurs distributions de probabilités. Si on suppose que l’agent dispose de relations de préférence et d’indifférence sur les conséquences des loteries, ces relations suffisent à caractériser le comportement de l’agent face au risque. Ces relations de préférence doivent respecter les cinq axiomes de Von Neumann-Morgenstern :
- Comparabilité, soit p et q deux distributions de probabilités :8p, q soit p  q soit p Á q soit p » q
- Transitivité :8p,q,zsipÂqetqÂzalorspÂz
- Indépendance :8p,q,z,8®2[0, 1] sipÂqalors®pÅ(1¡®)z®qÅ(1¡®)z
- Continuité :8p,q,zsipÂqÂzalors9®,¯2[0, 1] tels que®pÅ(1¡®)zÂq¯qÅ(1¡¯)z
- Rangement :
Notons L(x, z : ®) une loterie avec la probabilité ® d’obtenir x et la probabilité (1 ¡®) d’obtenir z. alors si x º y º z et x º u º z alors si y » L(x, z : ®1) et u » L(x, z : ®2) alors si ®1È ®2alors y  u ; si ®1Æ ®2alors y » u
Avec ces cinq axiomes et l’hypothèse que les agents préfèrent la richesse, nous obtenons la théorie de l’utilité espérée et caractérisons l’attitude de l’agent face au risque.
Le paradoxe de Allais remet en cause la théorie de l’utilité espérée, car il viole l’axiome d’indépen-dance.
10 Primes de risque
Pour toute fonction d’utilité concave, on a l’inégalité de Jensen :
E(U (W ))ÇU (E(W ))
Afin de calculer la prime de risque de Markowitz, on calcule d’abord l’équivalent certainWeq :
U (W eq)Æ E(U (W ))
La prime de risque de Markowitz, ¼ vaut :
¼ Æ E(W )¡W eq
c’est la somme que l’agent est prêt à payer pour éviter le risque. Ici :
E(W )Æ(1ÅE(RA)£W Æ1113
U (E(W ))Æ10Å20l n(1113)Æ150, 29
E(U (W ))Æ150, 25
On vérifie bien l’inégalité de Jensen : E(U (W )) ÇU (E(W )).
On calcule l’équivalent certain tel que : l n(Weq ) Æ 150, 25 soit Weq Æ 1110, 35 ". Ainsi la prime de Markowitz vaut : ¼ Æ E(W ) ¡Weq Æ 2, 65 "
La formule pour la prime de risque d’Arrow-Pratt est :
¼Æ 1¾2AR A
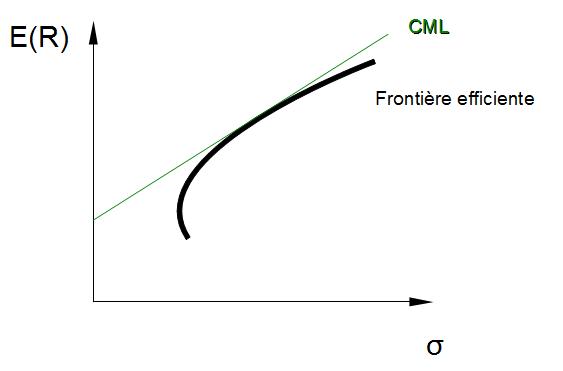
11 Frontière efficiente sans actif sans risque
L’équation générique de la frontière efficiente de Markowitz dans le plan (écart-type, espérance de rendement) :
V (Rp)Æ aE(Rp)2ÅbE(Rp)Åc
S’il n’y a pas d’actif sans risque.
…
Pour obtenir un portefeuille d’espérance de rendement E(Rj ), on prendra [1 ¡E(Rj )] de g et E(Rj ) de g Åh Æ) E(Rp ) Æ g ÅhE(Rj )
12 Frontière efficiente avec un actif sans risque
Avec un actif sans risque, le programme pour obtenir la frontière efficient s’écrit :
…
(R ¡Rf ) ¡[XT (R ¡Rf ]-X [xT -X ]¡1 Æ 0
…
Ici nous devons résoudre le système de trois équations à trois inconnues : 8
<R1 ¡RfÆZ1¾11 ÅZ2¾12 ÅZ3¾13
R2¡R fÆ Z1¾21Å Z2¾22Å Z3¾23
: R3¡R fÆ Z1¾31Å Z2¾32Å Z3¾33
Soit 8
< 9 Æ 5Z1 Å4Z2 Å3Z3 7 Æ 4Z1 Å2Z2 Å5Z3
: 6 Æ 3Z1 Å5Z2 Å1, 5Z3
On trouve : Z1 Æ 1, 59 Z2Æ0, 23 Z3Æ0, 03
D’où : X1 Æ 0, 86 X2Æ0, 13 X3Æ0, 02
E(RM)Æ X1R1Å X2R2Å X3R3
V (RM)Æ X12¾11Å X22¾22Å X32¾33Å2X1 X2¾12Å2X1 X3¾13Å2X2 X3¾23
Finalement : E(RM ) Æ 9, 7 et ¾(RM ) Æ 2, 16
Ce qui nous donne la CML :
|
E(Rp)Æ R fÅ |
E(RM)¡R f |
¾(Rp) |
|
¾(RM) |
13 Portefeuille d’arbitrage
13.1 Enoncé
On considère un actif sans risque de rendement 1% et le tableau d’espérance et de covariance suivant (exprimé en pourcentages) :
|
A |
B |
C |
|
|
Espérance |
10 |
9 |
7 |
|
A |
5 |
2 |
3 |
|
B |
2 |
0,5 |
|
|
C |
1,5 |
Vous avez identifié un portefeuille d’actions D avec un ¯D Æ 0, 2 et une espérance de rendement de 14%. Proposez si possible un portefeuille d’arbitrage en indiquant son excès de rendement ® et sa sensibilité au marché ¯.
13.2 Méthode
On calcule tout d’abord la SML :
E(Ri)Æ R fůi(E(RM)¡R f)
avec :¯iÆcov(R2i ,RM )
On calcule la composition du portefeuille de marché en actif A, B et C :
X AÆ6, 27 XBÆ1, 63 XCÆ ¡6, 9
On trouve avec ces pondérations les caractéristiques suivantes pour le portefeuille de marché :
E(RM)Æ29%
V (RM)Æ43, 41
|
Ainsi on peut calculer le ¯ du portefeuille B : ¯B Æ |
X A cov(RB,RA)ÅXB ¾B |
