Support de formation sur le calcul de capacité de condensateur

Découvrez comment résoudre ce problème dans ce chapitre.
Avec l’invention du générateur électrostatique vers 1660, on peut faire de nombreuses expériences avec l’électricité. Toutefois, on n’a pas de moyens d’accumuler des charges importantes. (On se rappelle que la pile électrique ne fut inventée qu’en 1800.)
La bouteille de Leyde
On cherchait donc un moyen d’accumuler des charges plus importantes, ce qu’on parvint à faire de manière un peu accidentelle. Le premier à le faire fut Ewald von Kleist en octobre 1745. Il fut suivi l’année suivante par un groupe de savants de l’université de Leyde aux Pays-Bas formé de Andreas Cuneus, Jean-Nicolas-Sébastien Allamand et Pieter van Musschenbroek (le plus important des trois). Au départ, on utilise une bouteille remplie d’eau, fermée avec un bouchon. À travers ce bouchon, il y a une tige de métal qui touche à l’eau. On touche à un générateur électrostatique avec la tige en métal tout en tenant la bouteille avec sa main. On éloigne ensuite la bouteille du générateur. Quand on touche la tige de métal avec l’autre main, on est secoué par une violente décharge électrique (van Musschenbroek pensa même qu’il allait en mourir). Le choc pouvant être assez fort, on préférait parfois regarder l’effet sur quelqu’un d’autre. C’est pour ça que la femme de Johann Winkler eut de la difficulté à marche pendant une journée après avoir reçu un choc…
?page=condensateurs1
On avait donc réussi à accumuler des charges dans la bouteille. À l’époque, on disait qu’on était parvenu à condenser le fluide électrique dans un contenant. On appela donc ce contenant un condensateur.
Ce condensateur ne fonctionnait pas toujours. On observe assez rapidement qu’on doit tenir la bouteille avec une main durant la charge et la décharge pour subir le choc en touchant à la tige avec l’autre main. On peut comprendre assez facilement pourquoi avec l’explication suivante : si on suppose que le générateur envoie des charges négatives dans l’eau, la main qui tient la bouteille, en contact avec
le sol par le corps, va se charger par ?page=condensateurs1 induction pour devenir positive. Si on éloigne ensuite la bouteille du générateur, l’eau reste négative et la main reste positive. Quand on touche à la tige de métal négative avec l’autre main, on a alors une main positive (celle qui tient la bouteille) et une main négative (celle qui touche à la tige), ce qui occasionne le passage de charges électriques à travers le corps.
Assez rapidement, on améliore le condensateur pour qu’il accumule plus de charges. L’abbé Nollet découvre aussi que l’eau est inutile et qu’on peut la remplacer par du métal ou un autre liquide, sauf de l’huile, ce qui laisse penser que l’eau joue simplement un rôle
de conducteur. On a donc l’idée de remplacer l’eau par des grenailles de plomb, puis par de minces feuilles d’étain, d’argent ou d’or chiffonnées, puis par une simple feuille métallique recouvrant la surface interne de la bouteille.
On découvrit également que la main de l’expérimentateur qui tient le condensateur ne joue qu’un rôle de conducteur et qu’elle peut être remplacée par une feuille métallique. On obtient alors un condensateur ressemblant à la figure de droite. Ce condensateur n’est qu’une bouteille recouverte d’une feuille métallique sur les surfaces interne et externe. Dès lors, il n’était plus nécessaire de tenir la bouteille avec la main pour qu’elle se charge, mais on devait relier la feuille de métal externe au sol. Si on connecte ce condensateur à un générateur électrostatique donnant des charges positives (figure de ?page=condens gauche), alors la feuille ateurs1
métallique intérieure se charge positivement et la feuille métallique extérieure se charge par induction avec une charge identique, mais de signe opposé.

On donna aussi le nom de bouteille de Leyde à ce condensateur parce que c’est à Leyde (Pays-Bas) que van Musschenbroek fit ses découvertes et parce que c’est surtout lui qui fit découvrir au monde cette invention. On donna aussi le nom d’armature à chacune des feuilles qui se charge.
Le condensateur peut prendre n’importe quelle forme.
L’abbé Nollet montra qu’on pouvait réussir à accumuler des charges même si la bouteille n’était pas fermée avec un bouchon. On pouvait réussir tout aussi bien avec une bouteille qu’avec un vase de verre. Il devenait évident que le condensateur ne doit pas nécessairement être une bouteille.
Dès 1748, Benjamin Franklin propose une forme complètement différente : le condensateur plat. C’était une simple plaque de verre recouverte d’une feuille métallique de chaque côté, ce qui nous donne un condensateur à plaques parallèles (figure). C’est le condensateur ayant la forme la plus simple.
La « batterie » de condensateurs
En reliant en parallèle plusieurs bouteilles de Leyde comme sur la figure, on pouvait accumuler beaucoup de charges.
Franklin donna le nom de batterie à un tel groupe de condensateurs en faisant l’analogie avec une batterie de canons qui est formée de plusieurs canons. (Plus tard, on utilisera aussi le terme batterie pour un groupe de piles chimique.)
La folie des chocs électriques (fin du 18e siècle)
Avec les condensateurs, on pouvait donner des chocs très importants. On observa alors des effets intéressants. Benjamin Franklin tua un dindon, alors que d’autres ramenèrent à la vie un moineau mort noyé.
Ces résultats firent sensation et il y eut une véritable mode des chocs électrique entre 1750 et 1800 en Europe. Tous voulaient ressentir cette nouvelle sensation. On faisait la file chez l’abbé Nollet pour recevoir une décharge de condensateur. Pour gagner du temps, l’abbé eut alors l’idée de donner le choc électrique en même temps à plusieurs personnes qui se tenaient la main. Cela aboutit finalement à des démonstrations spectaculaires : une fois, on donna un choc à une compagnie de 180 soldats à la cour de Louis XV et, une autre fois, à une congrégation de chartreux formant une ligne de 1800 m ! On alla aussi jusqu’à vendre des condensateurs en verre en forme de canne qui permettaient de donner des chocs à d’autres personnes pour faire une bonne blague. Une de ces blagues a dû mal tourner, car elle fut à l’origine d’un duel entre le chevalier Versac et la Chenaudière.
Plusieurs affirmèrent aussi qu’on pouvait guérir de nombreuses maladies à l’aide de choc électrique donné par des bouteilles de Leyde. Puisque le fluide électrique peut aller partout dans le corps, on voulait mélanger le fluide électrique aux médicaments pour que ceux-ci puissent aller partout dans le corps. Pour l’abbé Berthollon, on pouvait guérir presque tout avec un bon choc électrique.
Définition
Un condensateur est simplement formé de deux armatures conductrices ayant des charges opposées, séparées par du vide ou un isolant. Par exemple, ce pourrait être deux plaques métalliques parallèles portant des charges opposées, séparées par du vide ou de l’air.
Nous étudierons en premier les condensateurs où il y a du vide entre les armatures. Nous examinerons plus tard les effets de la présence d’un isolant entre les armatures.

Puisqu’il y a un champ électrique entre les deux armatures, cela veut dire qu’il y a une différence de potentiel entre les armatures. Le lien entre la charge des armatures et la différence de potentiel entre les armatures est la capacité du condensateur, notée C.
| Capacité d’un condensateur | Q C V= ∆ |
Cette définition de la capacité fut donnée par Volta à la fin du 18e siècle.
Notez qu’on prend la valeur absolue des charges des plaques et la valeur absolue de la différence de potentiel entre les armatures.
On voit que plus la capacité d’un condensateur est grande, plus il y aura de charge sur chacune des armatures pour une même différence de potentiel.
Les unités de la capacité sont des C/V. On a donné le nom de farad à cette unité.
| Le farad (F) | 1F =1VC |
Le farad est une unité très grande et les condensateurs ont généralement des capacités qui sont souvent données en µF (microfarad = 10-6 F), en nF (nanofarad = 10-9 F) ou en pF (picofarad = 10-12 F).
Formules de la capacité
Trouvons maintenant la capacité de trois types de condensateurs. Pour y arriver, il faut supposer que le condensateur est chargé. En trouvant alors la différence de potentiel entre les armatures, on pourra trouver la capacité avec

Q
C =
∆V
Condensateur à plaques parallèles
Avec une plaque chargée positivement et une plaque chargée négativement, le champ entre les plaques est, selon les chapitres précédents,
σ Q
E = = ε ε0 A 0
où A est l’aire d’une plaque. Cette charge Q est la valeur absolue de la charge de chacune des plaques.
La différence de potentiel entre les plaques est
∆V = Ed
Q

= d
Aε0
La capacité est donc
Q Q
C= =
∆V Qd
Aε0
Ce qui donne
| Capacité d’un condensateur à plaques parallèles A C =ε0  d |
On voit donc que la capacité augmente avec l’aire des armatures. On voit aussi que la capacité augmente quand on diminue la distance entre les armatures
Déjà avec les bouteilles de Leyde, William Watson avait découvert que la charge accumulée est proportionnelle de la surface du vase (qui est l’équivalent de l’aire des plaques pour un condensateur à plaques parallèles) et inversement proportionnelle à l’épaisseur du verre (qui est l’équivalent de la distance entre les plaques pour un condensateur à plaques parallèles).
On peut finalement constater que l’unité de ε0 peut aussi être des F/m puisque la capacité est en F et A/d est en m.
| Exemple 7.2.1 Un condensateur à plaques parallèles est formé de deux plaques de 2 cm x 3 cm séparées d’une distance de 1,5 mm ? a) Quelle est la capacité de ce condensateur ? La capacité est A C =ε0 d  (0,02m×0,03m) = 8,854×10−12mF 0,0015m = 3,54×10−12F = 3,54pF b) Quelle est la charge des plaques si la différence de potentiel entre les plaques est de 1200 V ? La charge est Q = ∆C V = 3,54×10−12F ×1200V = 4,25nC Ce qui veut dire que la plaque positive a une charge de 4,25 nC et la plaque négative a une charge de -4,25 nC.  |
Notez que si on voulait un condensateur de 1 F, il faudrait des plaques ayant une aire de 1,13 X 108 m² si elles sont séparées de 1 mm. Ce sont des plaques carrées d‘un peu plus de 10 km de côté !
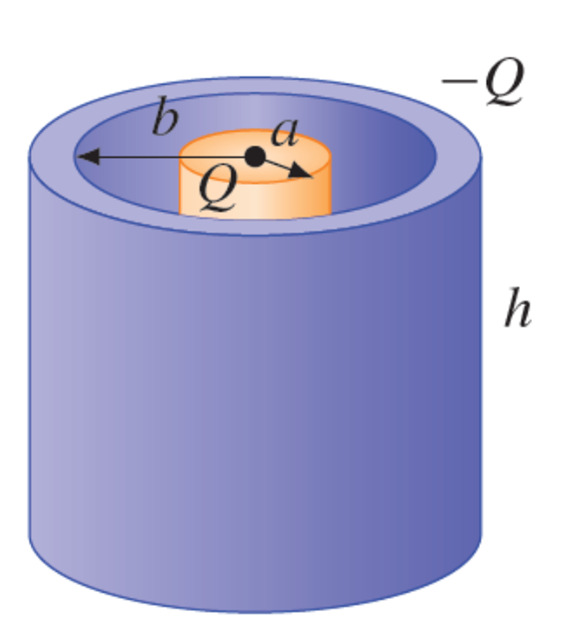
Condensateur cylindrique
Le condensateur cylindrique est formé de deux cylindres conducteurs emboités l’un dans l’autre séparés par de l’air, comme sur la figure.
Le calcul de la capacité sera plus compliqué ici et on le fait pour illustrer comment se fait le calcul de la capacité dans des situations plus complexes. Toutefois, vous n’aurez pas à refaire ce genre de calcul.
On suppose premièrement qu’une armature (on choisit le cylindre plein à l’intérieur) a une charge positive et que l’autre armature (le tuyau externe) a une charge positive.
Notre plan de match est le suivant.
1) Trouver le champ électrique entre les armatures.
2) Trouver la différence de potentiel entre les armatures (à partir du champ) 3) Trouver la capacité (à partir de la différence de potentiel)
1)Trouver le champ électrique entre les armatures.
Ici, le champ entre les armatures n’est pas uniforme. On peut cependant le trouver avec le théorème de Gauss puisqu’il y a symétrie cylindrique. Si on fait un cylindre de Gauss de rayon r passant entre les deux armatures, on a
Qint

E2πrh =
ε0
Si notre cylindre de Gauss a une longueur h, on a
λh E2πrh =
ε0
λ E =
2πεr0
où λ est la densité de charge de la tige interne, car il n’y a que cette armature à l’intérieur de la surface de Gauss.
Puisque sa densité de charge est
Q
λ= ℓ
Le champ est
Q
E =
2π εrℓ0
2)Trouver la différence de potentiel entre les armatures.
Puisque le champ change continuellement, la différence de potentiel entre les armatures se trouve avec
∆ =−V ∫ Edrcosθ
Le déplacement est dr puisqu’on se déplacera d’une armature à l’autre dans la direction radiale, en allant de r = a à r = b. La différence de potentiel est donc
b
∆ =−V ∫a 2π εQrℓ 0 dr cos0°
L’angle est 0° puisqu’on se déplace en s’éloignant de l’axe des cylindres et le champ est aussi en s’éloignant de l’axe des cylindres (voir figure). On obtient donc
Q b 1 ∆ =−V ∫ r dr
2πεℓ 0 a
Q b

=− 2πεℓ 0 [lnr]a
Q
=− (lnb −lna)
2πεℓ 0
Q b
=− ln
2πεℓ0 a
On laisse tomber le signe négatif, car c’est la valeur absolue de la différence de potentiel qui nous intéresse.
3) Trouver la capacité.
La capacité est
Q C =
∆V
Q

=
Q b ln
2πεℓ 0 a
En simplifiant, on a
| Capacité d’un condensateur cylindrique 2πεℓ C= 0ln(b a/ ) |
| Capacité d’un condensateur sphérique ab C = 4πε0 b − a |
Condensateur sphérique

Le condensateur sphérique est formé de deux armatures sphériques ayant le même centre, séparé par de l’air.
On va vous épargner le détail de calcul de la capacité. La procédure ressemble beaucoup à ce qu’on a fait pour le condensateur cylindrique.
Le résultat est
On peut même trouver la capacité d’une seule sphère. C’est en fait un condensateur sphérique, mais avec le rayon de l’armature externe (celle de rayon b) qui tend vers l’infini. C’est comme si le reste de l’univers jouait le rôle de la sphère externe. La capacité est donc
ab
C = lim4πε0b→∞b − a
Ce qui nous donne
| Capacité d’une sphère de rayon a | C = 4πε0a |
Par exemple, la Terre a une capacité de
C = 4π×8,854 10× −12mF ×6,38 10× 6m

C = 710µF
| Exemple 7.2.2 Un ballon de 10 cm de rayon est chargé jusqu’à ce que son potentiel atteigne 50 000 V. Quelle est la charge sur le ballon ? La capacité du ballon est C= 4πε0a = 4π×8,854×10−12mF ×0,1m=11,1pF La charge est donc Q = C V∆ =11,1 10× −12F ×50000V = 5,5 10× −7C = 0,55µC |
On peut utiliser des condensateurs dans des circuits. Voici à quoi peut ressembler cette composante.

(Elektrotechnik)
Symbole du condensateur
On utilise le symbole suivant pour le condensateur.
De toute évidence, on s’est inspiré des condensateurs à plaques parallèles.
Circuit avec une source et un condensateur
Si on branche un condensateur à une pile, on a le circuit suivant.
Dans ce cas, les plaques du condensateur vont commencer à se charger quand on va fermer l’interrupteur jusqu’à ce que la différence de potentiel entre les plaques soit la même que celle entre les bornes de la source.
Pendant que le condensateur se charge, le courant est le même de chaque côté du condensateur. Il y a des charges positives qui arrivent sur une des armatures, ce qui lui donne une charge positive, pendant qu’il y a des charges positives qui quittent l’autre armature, ce qui lui donne une charge négative. Les courants de chaque côté du condensateur sont égaux parce que pour un condensateur dans un circuit, les deux armatures ont toujours des charges de même grandeur, mais de signes opposés. Si on donne une certaine quantité de charge chaque seconde sur une armature, on doit enlever le même nombre de
charge par seconde sur l’autre armature, ce qui signifie que les courants sont égaux. Notons que les armatures ont nécessairement des charges identiques, mais de signes opposés parce que si ce n’était pas le cas, il y aurait un champ électrique à l’extérieur du condensateur qui attirerait ou repousserait des charges vers les armatures. Ce processus continuerait jusqu’à ce qu’il n’y ait plus de champ, donc jusqu’à ce que les armatures aient la même charge.
Une fois que la différence de potentiel aux bornes du condensateur est égale à celle aux bornes de la source, les charges sur les armatures ne changent plus. Il n’y a donc plus de charges qui arrivent à la plaque positive, ce qui signifie que le courant est nul. On en conclut ainsi que le courant sur une branche est nul à l’équilibre (ce qui veut dire que les condensateurs ont eu le temps de se charger) s’il y a un ou plusieurs condensateurs sur cette branche.
On peut aussi appliquer les méthodes vues aux chapitres précédents pour trouver la charge des condensateurs avec des circuits un peu plus complexes.
Branchement de deux condensateurs ensemble
Voyons ce qui arrive si on branche deux condensateurs ensemble et qu’au moins un des condensateurs est chargé. Initialement, on a
Notez que dans cette situation, les charges ne peuvent se déplacer d’un condensateur à l’autre parce que l’interrupteur est ouvert sur un des fils reliant les condensateurs. Elles ne peuvent pas se déplacer non plus du côté où il n’y a pas d’interrupteur, car les charges des armatures sont toujours identiques, mais de charges opposées. Ainsi, si les charges positives ne peuvent se déplacer sur notre figure, les charges négatives ne peuvent pas se déplacer aussi.

Quand on ferme l’interrupteur, les charges pourront alors passer d’un condensateur à l’autre. On aura alors
On peut trouver les nouvelles charges de chaque condensateur avec les deux conditions suivantes.
Première condition
Dans ce cas, la différence de potentiel aux bornes des condensateurs doit être égale.
∆V1 = ∆V2
Puisque la différence de potentiel aux bornes d’un condensateur est ∆V = Q/C Cela signifie que
Q1′ = Q2′
C1 C2
Deuxième condition
Les charges sur les plaques des condensateurs vont donc se déplacer d’un condensateur à l’autre pour que les différences de potentiel deviennent égales.
Il faut toutefois faire attention à la façon dont les condensateurs ont été branchés.
Regardons ce qui arrive si on branche ensemble les armatures de mêmes signes. On va se concentrer sur ce qui se passe dans le fil du haut. En fermant l’interrupteur, on met en contact les charges positives du condensateur de gauche et les charges positives du condensateur de droite et c’est toutes les charges qui vont se redistribuer. On aura alors
Q1 +Q2 = Q1′+Q2′
Regardons ce qui arrive si on branche ensemble les armatures de signes contraires. On va se concentrer sur ce qui se passe dans le fil du haut. En fermant l’interrupteur, on met en contact les charges positives du condensateur de gauche et les charges négatives du condensateur de droite et c’est toutes ces charges qui vont se redistribuer. On aura alors

Q1 −Q2 = Q1′+Q2′
(Prenez toujours Q1 comme la charge du condensateur ayant la plus grande charge.)
| Exemple 7.3.2 Un condensateur de 10 µF est chargé avec une source de 72 V et un condensateur de 5 µF est chargé avec une source de 96 V. Que devient la charge de chaque condensateur si on branche les deux condensateurs… a) en reliant ensemble les armatures de mêmes signes ? Les charges initiales des condensateurs sont |
| Q1 = C1∆V1 =10µF ×72V = 720µC Q2 = C2∆V2 = 5µF ×96V = 480µC Pour trouver les charges après le branchement, nos deux conditions sont Q1′ = Q2′ C1 C2  Q1′ = Q2′ 10µF 5µF et Q1 +Q2 = Q1′+Q2′ 1200µC = Q1′+Q2′ On doit résoudre ces deux équations pour trouver la solution. En isolant Q'2 dans la deuxième équation et en remplaçant dans la première, on a Q1′ = 1200µC −Q1′ 10µF 5µF 5Q1′ =12000µC −10Q1′ 15Q1′ =12000µC Q1′ = 800µC  De là, on trouve facilement Q’2 1200µC Q Q= 1′+ 2′ 1200µC = 800µC Q+ 2′ Q2′ = 400µC Après le branchement, la différence de potentiel aux bornes des condensateurs est donc Q′ 800µC Q′ 400µC ∆V = 1 = = 80V ou ∆V = 2 = = 80V C1 10µF C2 5µF b) en reliant ensemble les armatures de signes contraires ? Pour trouver les charges après le branchement, nos deux conditions sont |
| Q1′ = Q2′  C1 C2 Q1′ = Q2′ 10µF 5µF et Q1 −Q2 = Q1′+Q2′ 240µC = Q1′+Q2′ On doit résoudre ces deux équations pour trouver la solution. En isolant Q'2 dans la deuxième équation et en remplaçant dans la première, on a Q1′ = 240µC −Q1′ 10µF 5µF 5Q1′ = 2400µC −10Q1′ 15Q1′ = 2400µC 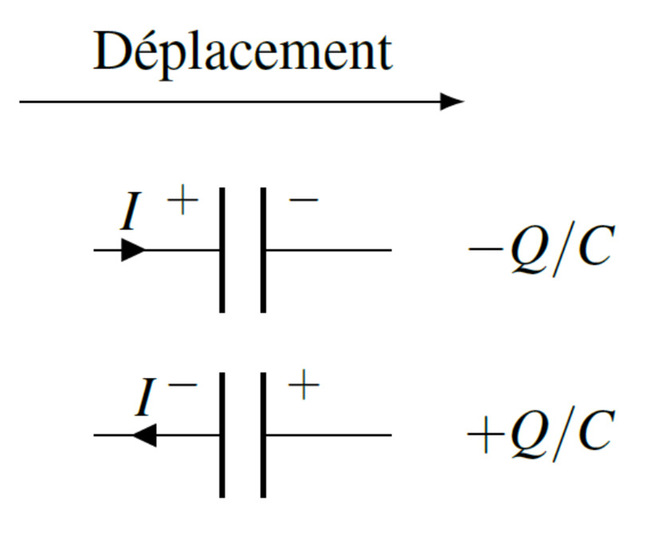 Q1′ =160µC De là, on trouve facilement Q'2 240µC Q Q= 1′+ 2′ 240µC =160µC Q+ 2′ Q2′ =80µC Après le branchement, la différence de potentiel aux bornes des condensateurs est donc Q′ 160µC Q′ 80µC ∆V = 1 = =16V ou ∆V = 2 = =16V C1 10µF C2 5µF |
Changement de capacité d’un condensateur
Il arrive parfois qu’on change la forme d’un condensateur. On pourrait, par exemple, éloigner ou approcher les plaques dans un condensateur à plaques parallèles. Ces changements modifient la valeur de la capacité et on pourra alors demander comment change la charge du condensateur ou comment change la différence de potentiel entre les armatures.
Pour répondre correctement à cette question, on doit savoir si notre condensateur est branché à une source ou non.

1) Il n’y a pas de source branchée aux armatures du condensateur
Dans ce cas, les armatures ne sont pas branchées et les charges ne peuvent quitter les armatures. On a donc
- Q ne change pas
- ∆V varie
2) Il y a une source branchée aux armatures du condensateur
Dans ce cas, la différence de potentiel entre les armatures reste constante et la source peut fournir ou enlever des charges. On a donc
- Q varie
- ∆V ne change pas
| Exemple 7.3.3 Un condensateur à plaques parallèles ayant une capacité de 1 µF est chargé de sorte que la différence de potentiel entre les plaques est de 100 V. Comment change la charge des plaques et la différence de potentiel entre les plaques si on double la distance entre les plaques… a) si les plaques ne sont pas branchées aux bornes d’une source ? 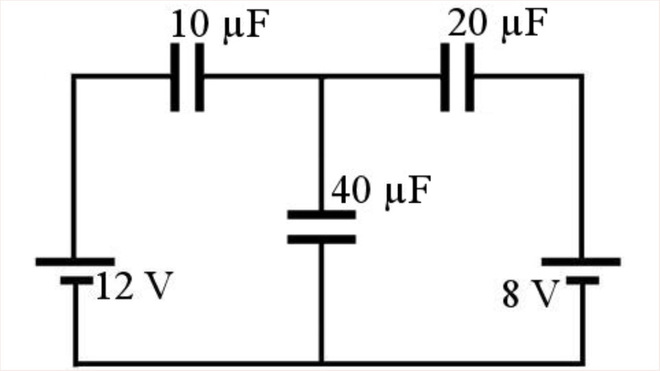 Trouvons premièrement la charge initiale des plaques du condensateur. Q C V= ∆ =1µF×100V =100µC Trouvons ensuite comment change la capacité du condensateur si les plaques sont deux fois plus loin. On sait que A 1µF =ε0 d Si les plaques sont maintenant à une distance 2d, on aura A 1 A 1 C′ =ε0 = ε0 = 1µF = 0,5µF 2d 2 d 2 Si les plaques ne sont pas branchées à une pile, Q ne changera pas et c’est la différence de potentiel qui changera. On aura donc  Q C V= ′∆ ′ 100µC = 0,5µF V×∆ ′ ∆V′ = 200V |
| On a donc Q′ = 100 µC et ∆V’ = 200 V b) si les plaques sont reliées aux bornes d’une source ? Si les plaques sont reliées à une source, la différence de potentiel reste toujours à 100 V. La charge sera donc Q′ = C′∆V = 0,5µF ×100V = 50µC On a donc Q′ = 50 µC et ∆V′ = 100 V |
Lois de Kirchhoff avec les condensateurs
La loi des mailles avec les condensateurs

On pourra utiliser les lois de Kirchhoff dans les circuits comportant des condensateurs. On doit donc savoir ce qu’on doit faire avec les condensateurs avec la loi de maille.
On pourrait croire qu’on peut facilement savoir si le potentiel monte ou diminue en regardant si on passe de l’armature positive à l’armature négative (le potentiel baisse dans ce cas) ou si on passe si de l’armature négative à l’armature positive (le potentiel monte dans ce cas). Le problème, c’est que le signe des charges des armatures n’est pas indiqué sur les circuits. On va donc supposer des charges pour les armatures. En faisant la solution des équations, si on trouve une valeur négative de Q, cela voudra simplement dire que les signes des charges des armatures sont le contraire de ce qu’on avait supposé. Ici, nous allons toujours supposer que l’armature qui reçoit le courant est l’armature positive.
Le courant qui arrive fait alors changer la charge du condensateur. Avec cette supposition, le courant fait augmenter la charge de l’armature positive et on a donc
dQ
I = dt
Les règles pour la loi des mailles sont donc
Dans le premier cas, la différence de potentiel est négative, car on passe de l’armature positive à l’armature négative alors que dans le deuxième cas la différence de potentiel est positive, car on passe de l’armature négative à l’armature positive.
Une variante de la loi des nœuds
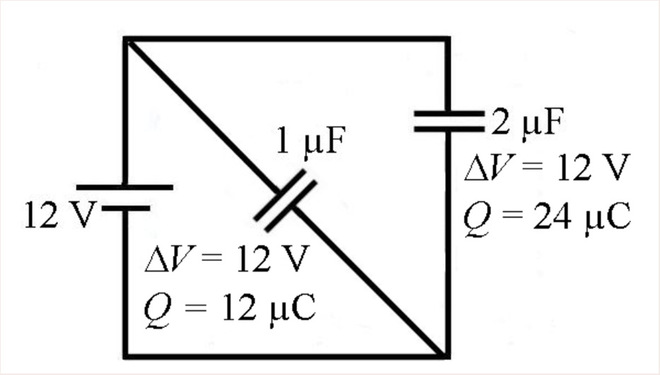
Supposons maintenant qu’on veuille savoir la charge des condensateurs de ce circuit.
La méthode utilisée précédemment dans laquelle on trouvait le potentiel des fils ne fonctionne pas parce qu’on ne peut pas trouver le potentiel à certains endroits sur la figure. De plus, il n’y a pas de condensateurs en série ou en parallèle, ce qui permettrait de simplifier le circuit comme on le fera dans la section suivante. On pourrait appliquer les lois de Kirchhoff pour trouver les charges des condensateurs, mais il n’y a pas de courant dans un circuit dans lequel il y a uniquement des condensateurs. Une fois que les condensateurs sont chargés, il n’y a plus de charges qui arrivent au condensateur, donc plus de courant dans les branches où il y a des condensateurs.
Toutefois, il y a eu des courants au départ pendant le bref instant durant lequel les condensateurs se sont chargés. On avait alors la situation suivante.

On avait alors, au nœud a,
I1 + I2 = I3
Or, ces courants chargeaient les condensateurs, ce qui veut dire que
dQ1 I2 = dQ2 I3 = dQ3
I1 =
dt dt dt
L’équation des nœuds devient donc
dQ1 + dQ2 = dQ3
dt dt dt
d Q( 1 +Q2 ) = dQ3
dt dt
Si on intègre, on obtient
Q1 +Q2 = Q3
En gros, avec des condensateurs, on fait notre loi des nœuds et on remplace les courants I par les charges Q et nous avons notre troisième équation pour résoudre le système. Appliquons cela ici
| Nous allons travailler avec les courants suivants (Il n’y a pas de courants une fois que les condensateurs sont chargés, mais ce furent les courants initiaux qui ont chargé les condensateurs.) Notre première loi des mailles se fera avec la maille de gauche. En partant du point a et en faisant le tour de la maille dans le sens des aiguilles d’une montre, on obtient, Q Q − 3 +12V − 1 = 0 40µF 10µF Notre seconde loi des mailles se fera avec la maille de droite. En partant du point a et en faisant le tour de la maille dans le sens contraire des aiguilles d’une montre, on obtient, Q Q 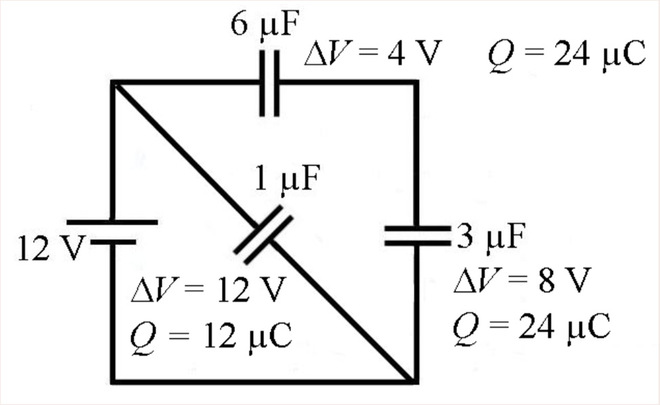 − 3 + +8V 2 = 0 40µF 20µF Finalement, notre loi des nœuds est I1 = I2 + I3 Qui signifie que Q1 = Q2 +Q3 Pour résoudre, on va isoler Q1 dans la première loi des mailles Q Q − 3 +12V − 1 = 0 40µF 10µF Q1 = − Q3 +12V  10µF 40µF Q1 = −0,25⋅Q3 +120µC |
| et on va isoler Q2 dans la seconde loi des mailles Q Q − 3 +8V + 2 = 0 40µF 20µF Q2 = Q3 −8V 20µF 40µF Q2 = 0,5⋅Q3 −160µC Pour finalement remplacer ces deux valeurs dans la loi des nœuds. On a alors Q1 = Q2 +Q3  −0,25⋅Q3 +120µC = 0,5⋅Q3 −160µC +Q3 −0,25⋅Q3 +120µC =1,5⋅Q3 −160µC 280µC =1,75Q3 Q3 =160µC On trouve alors les autres charges Q1 = −0,25⋅Q3 +120µC = −0,25 160⋅ µC +120µC = 80µC Q2 = 0,5⋅Q3 −160µC = 0,5 160⋅ µC −160µC = −80µC  Les charges des condensateurs sont donc les suivantes. Les signes des armatures sont indiqués selon notre convention : la plaque positive est du côté où le courant utilisé pour nos lois de Kirchhoff arrive si on obtient une réponse positive pour Q (c’est le cas ici pour les condensateurs 1 et 3). Si on a une réponse négative pour Q (c’est le cas ici pour le condensateur 2), c’est la plaque positive qui aurait été du côté où le courant utilisé pour nos lois de Kirchhoff arrive. |
Condensateurs en série
Supposons qu’on ait plusieurs condensateurs branchés en série tels qu’illustrés sur cette figure.
Montrons premièrement que tous les condensateurs vont acquérir la même charge quand ils sont en série. Pendant la charge, il y a un courant et on sait que ce courant doit être le même pour tous les éléments branchés en série.
Ainsi, chaque condensateur reçoit le même courant, ce qui veut dire que la charge de toutes les armatures change exactement au même rythme. On a donc
Charge des condensateurs en série
Tous les condensateurs branchés en série ont des charges identiques
À la fin de la période de charge, on aura donc la situation suivante.
réalité ce courant est nul puisque les condensateurs ont atteint leur charge à l’équilibre.) On aura alors
Q Q Q
E − − − = 0
C1 C2 C3
Q Q Q

E = + +
C1 C2 C3
Si on fait aussi la loi des mailles avec le circuit avec le condensateur équivalent, on a
Q
E − =0
Ceq
Q
E =
Ceq
En égalant les deux équations obtenues pour chaque circuit, on obtient
Q Q Q Q
= + +
Ceq C1 C2 C3
1 1 1 1
= + +
Ceq C1 C2 C3

On peut facilement extrapoler pour deviner la formule s’il y avait plus de trois condensateurs. On arrive alors à
| Condensateur équivalent : condensateurs en série 1 1 1 1 1 = + + + + Ceq C C1 2 C3 C4 |
Condensateurs en parallèle
Supposons qu’on ait plusieurs condensateurs branchés tels qu’illustrés sur cette figure.
Les courants qu’on voit sont les courants pendant la charge des condensateurs. La charge donnée par la source qui arrive au nœud (courant I) se sépare en 3 pour aller charger les condensateurs. Selon le principe de conservation de la charge et selon ce qui a été dit pour la loi des nœuds, on doit avoir que
Q = Q1 +Q2 +Q3
Comme tous les condensateurs sont branchés en parallèle avec la source, les différences de potentiel aux bornes des trois condensateurs sont égales à E . On a donc
Q = C1E E E+C2 +C3
On veut trouver un condensateur équivalent à ces trois condensateurs. Pour qu’il soit équivalent, il faut que les charges données par la source soient les mêmes avec le condensateur équivalent qu’avec les trois condensateurs. On doit donc avoir que
Q = CeqE

Puisque les charges doivent être égales, on a
On doit donc avoir que
CeqE E E E=C1 +C2 +C3
Ceq = + +C C C1 2 3
On peut facilement extrapoler pour deviner la formule s’il y avait plus de trois condensateurs. On arrive alors à
Condensateur équivalent : condensateurs en parallèle
Ceq = + + + +C1 C2 C3 C4
Exemples
Ces lois nous permettront de simplifier des circuits, ce qui nous aidera à déduire les charges dans chaque condensateur
| On a alors 2 condensateurs en parallèle. La résistance équivalente est Ceq2 =1µF+ 2µF Ceq2 = 3µF On a alors le circuit suivant.  La charge du condensateur équivalent est donc Q = Ceq2∆V = 3µF ×12V = 36µC On va maintenant reconstruire le circuit de départ en utilisant la charge du condensateur équivalent pour déduire la charge de chaque condensateur. On va commencer par remettre les deux condensateurs en parallèle. Quand on remplace un condensateur équivalent par des condensateurs en parallèle, la différence de potentiel aux bornes des condensateurs en parallèle est la même que la différence de potentiel aux bornes du condensateur équivalent. Il y aura donc 12 V aux bornes de chacun des condensateurs. Sachant la différence de potentiel, on peut alors trouver la charge des deux condensateurs. Q1µF =1µF ×12V =12µC Q2µF = 2µF ×12V = 24µC On a donc la situation suivante. Remarquez que la somme des charges des condensateurs en parallèle est la même que celle du condensateur équivalent. Il en sera toujours ainsi. On va ensuite remettre les deux condensateurs en série. Quand on remplace un condensateur équivalent par des condensateurs en série, la charge des condensateurs en série est la même que la charge du condensateur équivalent. La |
Il a fallu fournir une certaine quantité d’énergie pour charger un condensateur. Il faut faire un certain travail pour ajouter des charges négatives à une armature négative (puisque les charges se repoussent) et il faut faire un certain travail pour ajouter des charges positives à une armature positive. C’est cette énergie qu’on pourra récupérer en déchargeant le condensateur.

Quand on charge un condensateur, on enlève des charges à une armature pour la mettre sur l’autre armature. Normalement, la charge passe par des fils, mais on peut imaginer qu’on la fait passer directement d’une armature à l’autre ici. De toute façon, on a vu précédemment que le travail fait ne dépend pas de la trajectoire des charges.
Si on déplace une charge dq entre deux armatures qui sont à des potentiels différents, la variation d’énergie électrique est
dU = dq×∆V
Si on somme toutes les variations d’énergie électrique, en partant d’une charge nulle jusqu’à la charge finale Q, on a
Q Qq 1Q 1 q2 Q Q2
UC = ∆∫Vdq =∫0 C dq = C∫0 qdq = C 2 0 = 2C
En utilisant Q = C∆V, on obtient toutes les possibilités suivantes pour l’énergie électrique dans un condensateur.
| Énergie dans un condensateur Q2 1 Q V∆ = 1 C V∆ 2 UC = =  2C 2 2 |
On remarque la deuxième forme, qui est identique à ce qu’on avait obtenu, au chapitre 4, pour l’énergie d’un conducteur chargé.
Notez que l’énergie du condensateur est sous forme de champ électrique. Plus il est chargé, plus il y a du champ électrique entre les plaques, et plus il y a de l’énergie dans ce champ.
En passant, l’énergie totale des condensateurs d’un circuit est égale à l’énergie du condensateur équivalent.
| Exemple 7.5.2 Une sphère conductrice de 20 cm de rayon possède une charge 10 µC. Quelle est l’énergie électrique de la sphère ? La capacité de la sphère est C = 4πε π0a = 4 ×8,854 10× −12mF ×0,2m = 22,25pF L’énergie est donc 2 (10 10× −6C)2Q UC = = −12F = 2,25J 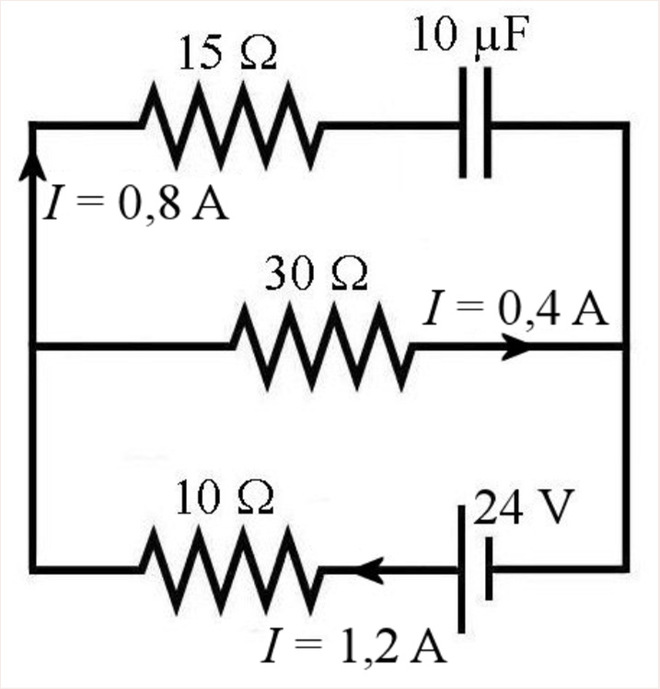 2C 2×22,25 10× (Cela est conforme au résultat obtenu au chapitre 4 qui donnait l’énergie d’un conducteur 1 1 kQ 1 9 10× 9 NmC²² × ×(10 10−6C)2 UE = QV = Q = = 2,25J) 2 2 R 2 0,2m |
Généralement, l’énergie dans un condensateur n’est pas très grande. Un condensateur de 1 farad (qui est une énorme capacité) chargé avec une différence de potentiel de 4,5 V, pourra à peine faire fonctionner une ampoule de 1 W (une lampe de poche) pendant une seconde, alors que trois piles de 1,5 V, qui donneront 4.5 V en série, pourront la faire fonctionner pendant des heures. Quel est l’intérêt alors d’utiliser des condensateurs s’ils ne peuvent pas emmagasiner beaucoup d’énergie ?
L’avantage des condensateurs, c’est qu’ils peuvent donner les charges très rapidement, ce qu’une batterie ne peut pas toujours faire à cause de sa résistance interne. Par exemple, il faut un courant intense, mais bref, pour faire fonctionner un flash de caméra et il est très difficile pour une batterie de donner un tel courant intense. On utilise donc la batterie pour charger lentement un condensateur. Quand il y a suffisamment de charges sur les armatures du condensateur, on utilise ces charges pour faire fonctionner le flash. On peut alors obtenir un fort courant très intense, mais qui dure peu de temps. La batterie recharge ensuite le condensateur et le processus peut recommencer. C’est ce qui explique le temps d’attente qu’il y a quand on prend des photos avec le flash : il faut attendre que le condensateur se recharge. Si on tentait de faire fonctionner directement le flash avec la batterie, elle devrait fournir un énorme courant et la différence de potentiel aux bornes de la batterie s’effondrerait puisqu’on perdrait tout le potentiel dans la résistance interne de la pile.
Il y a aussi des condensateurs dans les défibrillateurs. Typiquement, on aura un condensateur de 100 µF qui sera chargé avec une tension de 2000 à 4000 V (en fermant l’interrupteur K1 et en ouvrant l’interrupteur K2), pour une énergie maximale d’environ 400 J (les nouveaux modèles ont plutôt des énergies de 200 J). On pourra alors obtenir un courant intense et bref (en fermant l’interrupteur K2 et en ouvrant l’interrupteur K1). Il faut ensuite recharger le condensateur (en fermant l’interrupteur K1 et en ouvrant l’interrupteur K2), ce qui prendra environ 10 secondes, avant de recommencer.
Les microphones peuvent aussi être de simples condensateurs à plaques parallèles. En recevant un son, les variations de pression de l’air font bouger une des plaques du condensateur, ce qui change la distance entre les plaques. Cela change la capacité, et donc la charge des plaques. Le courant qui fournit les charges au condensateur va donc suivre les mêmes variations que le courant.
Circuit RC
La charge d’un condensateur
On va premièrement étudier le circuit suivant dans lequel un condensateur initialement vide se charge.
On veut connaître le courant en fonction du temps dans ce circuit à partir du moment où on ferme l’interrupteur (qui sera notre t = 0). On peut résoudre ce circuit avec la loi des mailles. On va commencer dans le coin inférieur droit et aller dans le sens des aiguilles d’une montre. On a alors
Q
E − RI − = 0
C
Comme le courant arrive au condensateur, il correspond aussi au rythme auquel les armatures
du condensateur accumulent les charges.
dQ
I = dt
On a donc l’équation suivante.
dQ Q
E − R − = 0 dt C
On doit donc résoudre cette équation pour connaitre la charge. Il s’agit d’une équation différentielle. Comme on n’est pas dans un cours d’équation différentielle, on va donner immédiatement la solution de cette équation. (Sachez que ce n’est pas une équation très difficile à résoudre.)
| Charge en fonction du temps pour un circuit RC (on charge le condensateur avec une source) −t Q = CE 1−eRC |
Dans l’exposant, on retrouve RC dont la valeur est en seconde. On appelle souvent cette combinaison la constante de temps du circuit et elle est notée τ.
Constante de temps d’un circuit RC
τ= RC
On a alors le graphique suivant pour la charge du condensateur en fonction du temps.
On ne peut donc pas répondre directement à la question « Combien faut-il de temps pour que le condensateur se charge ?» puisque la charge n’atteint jamais, en théorie, la charge complète. On peut cependant se donner une idée du rythme de charge en définissant la demi-vie du circuit comme le temps qu’il faut pour le condensateur ait 50 % de la charge maximale. On a alors
−t
Q = CE 1−eRC
CE = CE 1−e−RCt1/2
2
−t1/2
= −1 eRC
−t1/2
eRC =
−t1/2 = ln 1
RC 2
t1/2 = −RC ln
Comme –ln½ = ln (½)-1 = ln 2, on a
Demi-vie d’un circuit RC (on charge le condensateur avec une source)
t1/2 = RC ln 2
Voici ce que cette demi-vie veut dire pour la charge d’un condensateur. Si la demi-vie est de 5 secondes, on a
| 5 secondes → 10 secondes → 15 secondes → 20 secondes → | Q Q = max Q = Q = Q = | Q (il manque max pour atteindre la charge maximale) 2 Q  (il manque max pour atteindre la charge maximale) 4 Qmax pour atteindre la charge maximale) (il manque 8 Q (il manque max pour atteindre la charge maximale) 16 |
On voit qu’à chaque demi-vie, ce qui manque pour atteindre la charge maximale est divisé par deux.
On peut alors trouver le courant dans le circuit, car on sait que le courant est la dérivée de la charge. On a donc
−t d C E 1−eRC dQ
I = = dt dt

Ce qui nous donne
| Courant en fonction du temps pour un circuit RC (on charge le condensateur avec une source) E −t I = eRC R |
Ce qui nous donne le graphique suivant pour courant en fonction du temps.
Les différences de potentiel aux bornes des deux éléments du circuit sont donc
| −t ∆ = =VR RI E eRC | Q −t ∆ = =Vc E 1−eRC  C |
Examinons ce qui se passe dans ce circuit pour mieux comprendre ces résultats.
Circuit à t = 0
Immédiatement après la fermeture de l’interrupteur, le condensateur n’est pas chargé et on a la situation suivante.
(On a mis des valeurs uniquement pour simplifier l’explication.) À t = 0, toute la différence de potentiel de la source (12 V) se retrouve aux bornes de la résistance puisque la charge du condensateur est nulle (ce qui signifie que la différence de potentiel aux bornes du condensateur est nulle). Puisque le courant correspond au rythme de charge du condensateur, on a
dQ
= I
dt dQ E
=
dt R
(Ce qui signifie dans notre exemple que le condensateur se charge initialement à un rythme de 6 C/s.) Ceci doit être la pente du graphique de la charge à t = 0.

Ce sont donc les résistances qui imposent le rythme initial de charge du condensateur.
Ainsi, à t = 0, le courant est exactement le même que ce qu’on aurait s’il n’y avait pas de condensateur puisque ce dernier ne fait aucune différence de potentiel. Ce sera toujours le cas à t = 0 avec des circuits où les condensateurs sont initialement vides.
Circuit pendant la charge du condensateur
À mesure que le condensateur se charge, la différence de potentiel aux bornes du condensateur augmente. La différence de potentiel aux bornes du condensateur va passer de 0 V à 12 V dans notre exemple. Voici la situation quand la différence de potentiel aux bornes du condensateur est rendue à 8 V.
Comme la différence de potentiel est maintenant de 8 V aux bornes du condensateur, elle doit être de 4 V aux bornes de la résistance. À mesure que la charge monte, la différence de potentiel aux bornes du condensateur augmente et la différence de potentiel aux bornes de la résistance diminue puisque la somme des deux différences de potentiel doit être égale à celle de la source. C’est exactement ce qu’on peut voir sur les deux graphiques des différences de potentiel aux bornes de la résistance et du condensateur en fonction du temps.
Toutefois, puisque la différence de potentiel aux bornes de la résistance est RI, cela veut dire que le courant doit diminuer si la différence de potentiel aux bornes de la résistance diminue. Dans notre exemple, on voit que le courant n’est plus que de 2 A si la différence de potentiel aux bornes de la résistance est de 4 V.
Donc, à mesure que la différence de potentiel augmente aux bornes du condensateur, le courant diminue et le condensateur se charge à un rythme de plus en plus petit. C’est pour ça que la pente diminue continuellement sur le graphique de la charge en fonction du temps.
C’est ce qu’on peut voir sur le graphique de la charge en fonction du temps.
Circuit au bout d’un temps très long
Au bout d’un temps très long, la charge du condensateur a atteint sa valeur maximale et on a la situation suivante.
La différence de potentiel aux bornes du condensateur est maintenant de 12 V, ce qui veut dire qu’elle est de 0 V pour la résistance. S’il n’y a pas de différence de potentiel aux bornes d’une résistance, c’est que le courant est nul. Le courant est donc nul et le condensateur ne reçoit plus de charge, ce qui signifie que la charge du condensateur est maintenant stable. Ce sera d’ailleurs toujours le cas pour des circuits avec des condensateurs : au bout d’un temps très long, il n’y a plus de courant dans les fils où il y a un condensateur.

| 5s − ∆VR =100V e⋅ 10s = 60,65V c)le courant à t = 1 s ? Le courant est E e−t = 100V e10−1ss = 0,181mA I = RC R 500kΩ |
Au bout d’un temps très long, l’énergie dans le condensateur est
1 2 1 CE 2U = C V∆ =

2 2
puisque la différence de potentiel aux bornes du condensateur est la même qu’aux bornes de la source au bout d’un temps très long. Or, la pile a fait le travail
W Q= E E E E=(C ) =C2
On voit que l’énergie du condensateur n’est que la moitié du travail fait par la source. Bien sûr, l’autre moitié est perdue en chaleur dans la résistance. Il est quand même étonnant qu’il y ait toujours la moitié de l’énergie fournie par la source qui va dans le condensateur et l’autre moitié qui se perd en chaleur dans la résistance, peu importe les valeurs de R et C. (Les sceptiques peuvent calculer l’énergie perdue en chaleur dans la résistance en calculant l’intégrale suivante.
∞ ∞ 2 ∞ REeRC−t2dtU =∫0 Pdt =∫0 RI dt =∫0 R
pour se rendre compte qu’elle vaut ½CE ². Il faut faire une intégrale parce que la puissance change constamment parce que le courant change constamment.)
(Pour ceux qui insistent, voici cette intégrale :
)
La décharge d’un condensateur
On va maintenant étudier le circuit suivant dans lequel un condensateur se décharge à travers une résistance.
Évidemment, le condensateur possède une charge initiale Q sinon il ne se passerait rien. On veut connaître le courant en fonction du temps dans ce circuit à partir du moment où on ferme l’interrupteur.

On peut quand même prévoir un peu ce qui va se passer. Pendant que le condensateur se vide, la différence de potentiel aux bornes du condensateur va baisser, ce qui fait que la différence de potentiel aux bornes de la résistance diminue parce que les différences de potentiel aux bornes du condensateur et de la résistance doivent être égales (en valeur absolue) selon la loi des mailles. Si la différence de potentiel aux bornes de la résistance diminue, cela veut dire que le courant dans le circuit diminue en fonction du temps. Voyons si c’est ça qui se passe.
On peut résoudre ce circuit avec la loi des mailles. On va commencer dans le coin inférieur droit et aller dans le sens des aiguilles d’une montre. On a alors
Q
−RI − = 0 C
Comme le courant arrive au condensateur (selon nos suppositions des lois de Kirchhoff), il correspond aussi au rythme auquel les armatures du condensateur accumulent les charges.
dQ
I = dt
On a donc l’équation suivante.
dQ Q
−R − = 0 dt C
On doit donc résoudre cette équation pour connaitre la charge. Encore, une fois, comme on n’est pas dans un cours d’équation différentielle, on va donner immédiatement la solution

de cette équation. (Celle-ci est encore plus facile à résoudre.)
| Charge en fonction du temps pour un circuit RC (décharge du condensateur) −t Q = Q e0 RC |
On a alors le graphique suivant pour la charge du condensateur en fonction du temps.
Encore une fois, on ne peut donc pas répondre directement à la question Combien faut-il de temps pour que le condensateur soit vide ? puisque la charge n’est jamais nulle en théorie. On peut cependant se donner une idée du rythme de décharge en définissant la demi-vie du circuit comme le temps qu’il faut pour le condensateur ait perdu 50 % de la charge initiale. On a alors
−t
Q = Q e0 RC
Q0 = Q e0 −RCt1/2
2
−t1/2

= eRC
1 −t1/2 ln =
2 RC
t1/2 =−RCln
Mais comme –ln½ = ln (½)-1 = ln 2, on a
Demi-vie d’un circuit RC (le condensateur se décharge à travers une résistance)
t1/2 = RCln2
Voici ce que cette demi-vie veut dire pour la charge d’un condensateur. Si la demi-vie est
de 5 secondes, on a
| 5 secondes → 10 secondes →  15 secondes → | Q = Q Q = 0 4 Q0 Q = |
Q
8
Q
20 secondes → Q = 0

16
On peut aussi trouver le courant dans le circuit, car on sait que le courant est la dérivée de la charge. On a donc
−t d Q e 0 RC dQ I = = dt dt
Ce qui nous donne
| Courant en fonction du temps pour un circuit RC (le condensateur se décharge à travers une résistance) Q0eRC−t I = RC |
(En fait, on obtient un courant négatif. Ceci vient de notre convention faite pour les lois de Kirchhoff qui stipulait que le courant arrivait à la plaque positive, comme si on chargeait le condensateur. Or ici, le condensateur se décharge et le courant quitte la plaque positive du condensateur. Il est donc normal qu’on arrive à une valeur négative de I dans cette situation puisque le courant est dans le sens contraire de celui supposé par la loi de Kirchhoff et il est donc dans le sens montré sur la figure. Comme on cherche ici la grandeur du courant, on oublie le signe négatif.)
Ce qui nous donne le graphique suivant pour courant en fonction du temps.
Avec un courant initial valant (on met t = 0 s dans l’équation du courant)

Q0
I0 =
RC
les différences de potentiel aux bornes des deux éléments du circuit sont donc
| Q −t ∆ = =VR RI 0 eRCC | Q Q −t ∆ = =Vc 0 eRC C C |
Ce qui nous donne les graphiques suivants.
On obtient exactement ce qui était prévu. Pendant que le condensateur se décharge, la différence de potentiel aux bornes du condensateur baisse, ce qui fait que la différence de potentiel aux bornes de la résistance diminue aussi, ce qui veut dire que le courant dans le circuit diminue.

| c) Quel est le courant à t = 1 s ? Le courant est Q0 eRC−t = 0,001C e10−1ss = 0,0905mAI = RC 10s |
Voici une petite note historique intéressante. Au 19e siècle, on commença à installer des câbles sous-marins pour transmettre des messages télégraphiques. C’était un simple fil métallique entouré d’une gaine isolante. Toutefois, quand on envoyait des signaux dans ces fils, le courant variait très lentement, ce qui faisait qu’il fallait un certain temps pour qu’on capte le signal à l’autre bout du fil. On remarqua cela pour la première fois en 1853 dans un câble sous-marin entre l’Angleterre et la Hollande. En fait, on venait de construire en circuit RC géant avec une énorme constante de temps. Pourtant, c’était un simple fil. Où est le condensateur ? Il ne faut pas oublier que l’eau salée est conductrice et qu’elle peut agir comme une armature. On avait donc un vaste condensateur cylindrique formé d’une armature qui était le fil métallique et d’une autre armature constituée de l’océan, séparé par la gaine isolante du fil. Quand on appliquait une différence de potentiel, le courant montait lentement comme dans un circuit RC et il ne montait pas assez vite pour qu’on puisse envoyer des signaux télégraphiques en faisant le code morse très rapidement comme on pouvait le faire à l’époque. Il fallait faire ce code très lentement, ce qui limitait le nombre de messages qu’on pouvait envoyer. On pouvait à peine faire 10 mots par minute.
Comme on voulait faire un câble transatlantique, il fallait résoudre ce problème. C’est Lord Kelvin qui analysa correctement ce qui se passait et proposa des solutions pour corriger cet effet. En partenariat avec une compagnie, il procéda à l’installation d’un fil transatlantique qui éliminait ce problème en 1867. C’est ce qui fit la fortune de Kelvin.
Courant à t = 0 et à t = ∞ dans des circuits plus complexes
Dans des circuits avec des condensateurs et des résistances, on peut déterminer les courants et les charges des condensateurs plus facilement à t = 0 et à t = ∞.
1) À t = 0 (on vient d’allumer la source ou de brancher les fils du circuit ou de fermer un interrupteur qui permet au courant de passer) avec des condensateurs initialement vides.
Dans ce cas, la différence de potentiel aux bornes des condensateurs vides est nulle et ils n’ont aucun effet dans le circuit puisqu’ils n’apparaitront pas dans les lois des mailles. Cela veut dire qu’on peut simplifier le circuit en remplaçant les condensateurs par des fils.
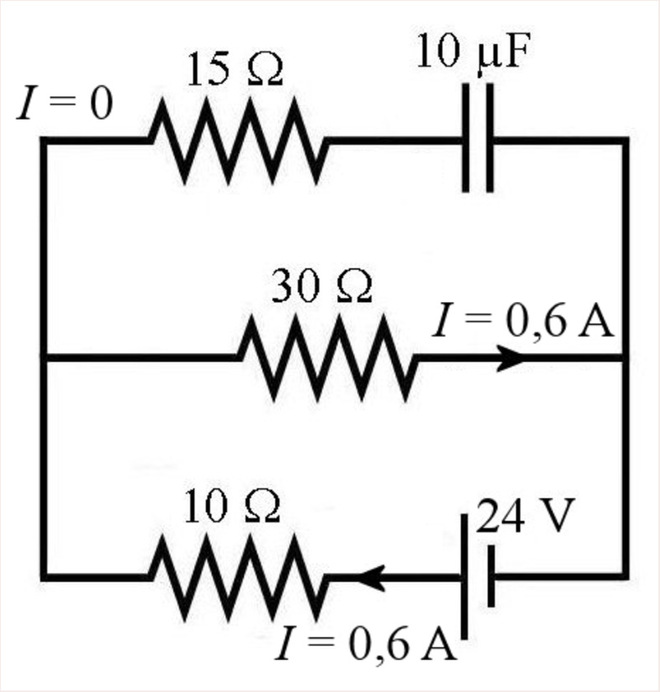
2) Au bout d’un temps très long (t = ∞).
À ce moment les condensateurs ont atteint leur charge d’équilibre et il n’y a pas de courant dans les branches sur lesquels il y a des condensateurs.

Dans ce cas, s’il n’y a plus de courant qui circule dans la branche sur laquelle il y a un ou des condensateurs, on peut enlever cette branche pour déterminer les courants puisqu’elle n’a plus d’effet dans la loi des nœuds.
−30Ω×0,6A+∆ − Ω× =Vc 15 0A 0
∆ =Vc 18V
La charge du condensateur est donc
Q C V= ∆ =10µF×18V =180µC
(Si vous aviez obtenu une réponse négative pour la différence de potentiel, n’oubliez pas que c’est la valeur absolue de la différence de potentiel qui va dans l’équation de la charge.)
Notez qu’un circuit a toujours une capacité même s’il n’y a pas de condensateur dans le circuit. Par exemple, le circuit suivant a une certaine
On peut mettre une substance diélectrique (donc isolante) entre les armatures d’un condensateur. L’introduction d’une telle substance a deux effets principaux
Augmentation de la capacité
Quand un diélectrique emplit tout l’espace entre les armatures, la capacité du condensateur augmente. L’augmentation est donnée par la formule suivante.
Augmentation de la capacité avec un diélectrique
C =κC0
où C est la capacité avec le diélectrique, C0 est la capacité quand il y a du vide entre les plaques et k est la permittivité relative.
Pour comprendre pourquoi la capacité augmente, on va examiner ce qui change si on fait entrer un diélectrique dans un condensateur à plaques parallèles. On se rappelle que la présence d’un diélectrique fait diminuer le champ électrique. La diminution est donnée par
E0
E = κ
Cette diminution du champ entre les plaques fait à son tour diminuer la différence de potentiel entre les plaques.
∆ =V Ed
Ed0
∆ =V
∆ =V
La différence de potentiel est donc divisée par la permittivité relative. La figure montre cette baisse de différence de potentiel pour un diélectrique qui a une permittivité relative de 2. On voit que la différence de potentiel est divisée par 2 quand on introduit le diélectrique entre les plaques d’un condensateur qui n’est pas branché à une source.
La capacité avec le diélectrique est
donc
Q C =

∆V
Q
=
()
Q
=κ
∆V0
=κC0
On voit donc que la capacité augmente puisqu’elle est obtenue en multipliant la capacité quand il y a du vide entre les plaques par la permittivité relative du diélectrique (qui est toujours plus grande que 1.)
Charge maximale du condensateur
On ne peut pas mettre autant de charge qu’on veut dans un condensateur.
Plus on charge les armatures, plus le champ électrique entre les armatures augmente. Si ce champ devient trop grand et dépasse la rigidité diélectrique de la substance séparant les armatures, la substance isolante va devenir conductrice et il va y avoir un courant d’une armature à l’autre, en fait une étincelle entre les armatures. Les électrons de l’armature négative vont alors se rendre à l’armature positive, ce qui va décharger les armatures.

On indique souvent sur le condensateur la différence de potentiel maximale qu’il peut y avoir entre les armatures. Sur la figure, on indique 12 000 V.
Notez qu’il y a aussi un champ électrique maximum dans le vide (autour de 25 MV/m, cela dépend de la forme des armatures). Il y a donc aussi une limite même s’il n’y a pas de diélectrique entre les armatures.
| Exemple 7.7.1 Il y a 1 mm de distance entre les plaques d’un condensateur à plaques parallèles. L’aire des plaques est de 1000 cm² et l’espace entre les plaques est empli de papier dont la permittivité relative est de 3,7 et la rigidité diélectrique est de 16 x 106 V/m. a) Quelle est la capacité de ce condensateur ? La capacité est C=κC0 A =κε0d = 3,7×8,854×10−12 mF 0,1 ²m 0,001m  = 3,276nF b) Quelle est la différence de potentiel maximale qu’il peut y avoir aux bornes de ce condensateur ? Il y a une valeur maximale de la différence de potentiel parce qu’il y a une valeur maximale pour le champ électrique entre les plaques. Ainsi, on a ∆Vmax =E dmax =16 10× 6 Vm×0,001m =16000V | ||
| c) Quelle est la charge maximale qu’il peut y avoir sur les plaques de ce condensateur ? Il y a une charge maximale parce qu’il y a une différence de potentiel maximale. On a donc Qmax = ∆C Vmax = 3,276nF×16000V = 52,5µC 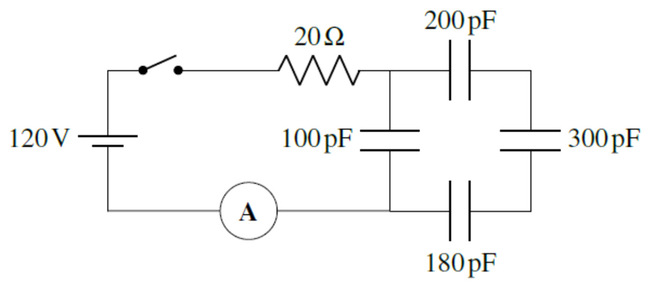 | ||
Il peut arriver que le diélectrique n’occupe pas tout l’espace entre les plaques, ou qu’il y ait plusieurs types de diélectriques entre les plaques. Voici comment on règle ce genre de problème pour des condensateurs à plaques parallèles.
Diélectriques qui n’occupent pas tout l’espace entre les armatures
Si les diélectriques sont en couche une au-dessus de l’autre entre les plaques, on va séparer le condensateur en condensateurs en série. Attention, la distance entre les plaques diminue quand on sépare le condensateur de cette façon, mais l’aire des plaques reste la même.
On va obtenir le même résultat puisque, pour des charges identiques sur les plaques, la différence de potentiel entre les plaques la plus basse et la plus haute sur la figure de droite est la même que celle entre les plaques de la figure de gauche, car il n’y a pas de différence de potentiel dans le morceau de conducteur qu’on a ajouté pour séparer le condensateur en deux.
On peut alors calculer la capacité de chacun de ces condensateurs avec la loi donnant la capacité d’un condensateur complètement empli de diélectrique.
On utilise ensuite la règle d’addition des condensateurs en série pour trouver la capacité totale.
| La capacité équivalente est donc 1 1 1 1 = + + C 3,542nF 1,771nF 6,198nFC = 0,992nF |
Si les diélectriques sont l’un à côté de l’autre entre les plaques, on va séparer le condensateur en deux condensateurs en parallèle. Attention, les grandeurs des plaques diminuent quand on sépare le condensateur de cette façon, mais la distance entre les plaques reste la même.
En réalité, les diélectriques ne sont pas des isolants parfaits, ce qui fait que les électrons de l’armature négative pourront passer lentement à travers le diélectrique pour aller annuler la charge positive de l’armature positive. Le condensateur va donc perdre lentement sa charge même s’il n’est pas branché à une résistance.

Le diélectrique agit donc aussi comme une résistance (très élevée). Sachez que ce condensateur est tout à fait équivalent à une résistance et un condensateur en parallèle puisque chacune des bornes de la résistance est branchée à une armature du condensateur. La différence de potentiel aux bornes de la résistance est donc la même que celle aux bornes du condensateur.
On aurait donc le circuit suivant si on tient compte de la résistance du diélectrique lors de la charge du condensateur.
La solution de ce circuit est plus complexe et fait appel un système d’équations différentielles. À titre de curiosité, la charge du condensateur en fonction du temps dans ce circuit est
R2 −R1+R2t
Q = CE R1 + R2 1−eR R C1 2
Capacité d’un condensateur
Q C V= ∆
Le farad (F)
1F =1VC
Capacité d’un condensateur à plaques parallèles
A
C =ε0 d

Capacité d’un condensateur cylindrique
2πε0ℓ
C= ln(b a/ )
Capacité d’un condensateur sphérique
ab
C = 4πε0 b − a
Capacité d’une sphère de rayon a
C = 4πε0a
Charge des condensateurs en série
Tous les condensateurs branchés en série ont des charges identiques.
Condensateur équivalent : condensateurs en série
1 1 1 1 1
= + + + +
CeqC C C C1 2 3 4

Condensateur équivalent : condensateurs en parallèle
Ceq = + + + +C1 C2 C3 C4
Énergie dans un condensateur
UC = Q2C2 = 12 12 2 Q V∆ = C V∆
Charge en fonction du temps pour un circuit RC (on charge le condensateur avec une source)
−t
Q = CE 1−eRC
Constante de temps d’un circuit RC
τ= RC
Demi-vie d’un circuit RC (on charge le condensateur avec une source)
t1/2 = RC ln2
Courant en fonction du temps pour un circuit RC (on charge le condensateur avec une source)
E −t
I = eRC
R
Charge en fonction du temps pour un circuit RC (le condensateur se décharge à travers une résistance)
−t
Q =Q e0 RC

Courant en fonction du temps pour un circuit RC (le condensateur se décharge à travers une résistance)
−t
Q0 eRCI =
RC
Augmentation de la capacité avec un diélectrique
C =κC0
7.2 La capacité
1. Quelle est la capacité de condensateur ?
2. Avec le condensateur à plaque parallèle suivant, déterminez…
a) la capacité du condensateur.
b) la charge de chaque plaque s’il y a une différence de potentiel de 100 V entre les plaques.
c) la grandeur du champ électrique entre les plaques.
3. En transférant 1013 électrons d’une armature à l’autre d’un condensateur qui n’était pas chargée initialement, il apparait une différence de potentiel de 24 V entre les plaques. Quelle est la capacité de ce condensateur ?
4. Avec le condensateur cylindrique suivant, déterminez…

a) la capacité de ce condensateur.
b) la différence de potentiel entre les armatures si l’armature positive a une charge de 1 nC et l’armature négative a une charge de -1 nC.
5. Dans ce condensateur sphérique, la charge de la plaque positive est de 50 nC et la charge de la plaque négative est -50 nC. La différence de potentiel entre les armatures est de 200 V et le rayon de la grande sphère est de b = 20 cm. Quel est le rayon de la petite sphère (a) ?
6. Dans un condensateur à plaques parallèles, la valeur absolue de la charge surfacique de chaque plaque est de σ = 40 nC/m². Quelle est la distance entre les plaques s’il y a une différence de potentiel de 20 V entre les armatures ?
7.3 Circuits simples avec des condensateurs
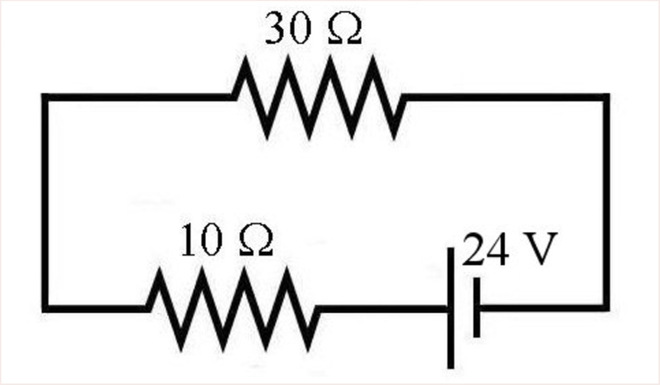
7. Quelle est la charge de chacun des condensateurs de ce circuit ? (Spécifiez aussi les signes des armatures.)
8. Quelle est la charge de chacun des condensateurs de ce circuit ? (Spécifiez aussi les signes des armatures.)
9. Un condensateur de 20 µF a été chargé avec une différence de potentiel de 12 V et un condensateur de 30 µF a été chargé avec une différence de potentiel de 32 V. On branche ensuite les condensateurs ensemble en reliant ensemble les armatures de même signe.
a) Quelles sont les charges des condensateurs après qu’on les ait branchés ensemble ?
b) Quelle est la différence de potentiel aux bornes de chaque condensateur après qu’on les ait branchés ensemble ?
10. Un condensateur de 40 µF a été chargé avec une différence de potentiel de 100 V et un condensateur de 20 µF a été chargé avec une différence de potentiel de 50 V. On branche ensuite les condensateurs ensemble en reliant ensemble les armatures de signe contraire.
c) Quelles sont les charges des condensateurs après qu’on les ait branchés ensemble ?

d) Quelle est la différence de potentiel aux bornes de chaque condensateur après qu’on les ait branchés ensemble ?
11. On charge un condensateur de 100 µF avec une différence de potentiel de 30 V. On branche ensuite ce condensateur avec un autre condensateur qui n’est pas chargé initialement. Après le branchement, la différence de potentiel aux bornes du condensateur de 100 µF diminue à 24 V. Quelle est la capacité de l’autre condensateur ?
12. Un condensateur à plaque parallèle de 36 µF est branché à une source de 12 V. La distance entre les plaques est initialement de 0,5 mm. De combien change la charge du condensateur et la différence de potentiel entre les armatures si on augmente la distance entre les plaques à 2 mm tout en laissant le condensateur branché à la source ?
13. Un condensateur à plaque parallèle de 36 µF est branché à une source de 12 V. On débranche ensuite le condensateur de la source et le condensateur reste chargé. La distance entre les plaques est initialement de 0,5 mm. De combien change la charge du condensateur et la différence de potentiel entre les armatures si on augmente la distance entre les plaques à 2 mm alors que le condensateur n’est toujours pas branché à la source ?
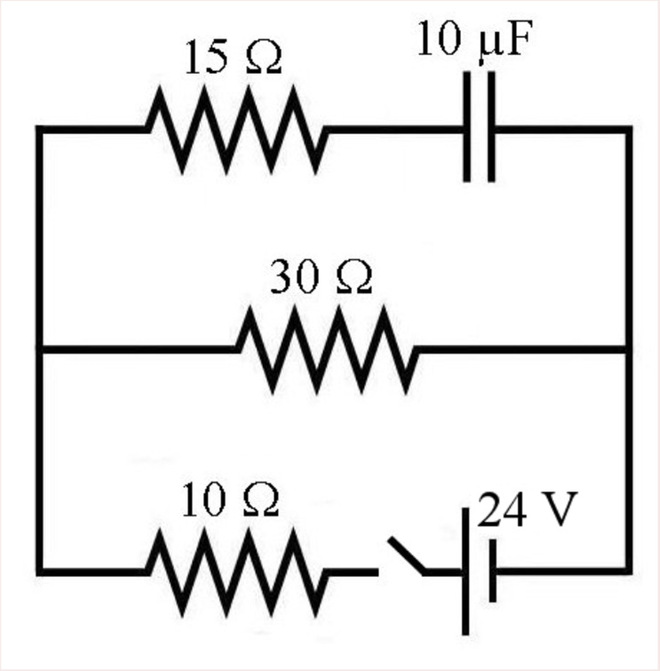
14. Quelles sont les charges des condensateurs de ce circuit ? (Spécifiez aussi les signes des armatures.)
15. Dans ce circuit, toutes les sources ont E = 10 V et tous les condensateurs ont une capacité de 5 µF. Quelle est la charge du condensateur identifié par un C dans ce circuit ? Indice : si vous pouvez trouver la bonne maille dans ce vaste circuit, vous pouvez facilement trouver la réponse.
-60-f-batteriesemf -10-v-charge-capacitor-c--q1151503
7.4 Les condensateurs en série et en parallèle
16. Quelle est la capacité équivalente de ce groupe de condensateurs ?
17. Quelles sont les charges de ces condensateurs ? (Spécifiez aussi les signes des armatures.)
18. Quelles sont les charges de ces condensateurs ? (Spécifiez aussi les signes des armatures.)
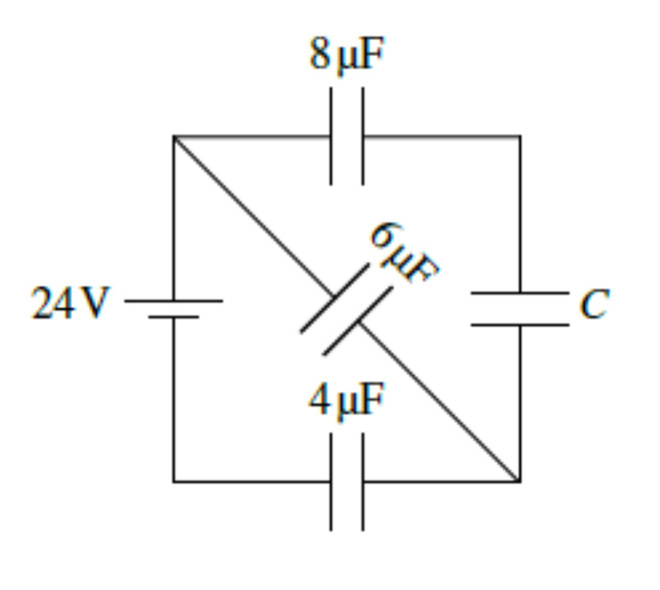
19. Quand la source a chargé ces condensateurs, elle a fourni une charge de 72 µC.
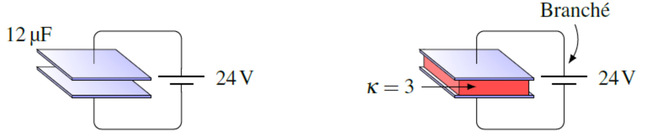
a) Quelle est la valeur de C ?
b) Quelle est la différence de potentiel aux bornes du condensateur C ?
7.5 L’énergie dans un condensateur
20. On charge un condensateur de 20 µF avec une différence de potentiel de 200 V. Quelle est l’énergie emmagasinée dans le condensateur ?
21. L’aire des plaques d’un condensateur à plaque parallèle est de 200 cm². Quelle doit être la distance entre les plaques si on veut accumuler 0,01 J dans ce condensateur quand on le charge avec une différence de potentiel de 500 V.
22. Quelle est l’énergie accumulée dans chacun de ces condensateurs ?
23. On charge un condensateur à plaque parallèle de sorte que l’énergie dans le condensateur est de 0,12 J. On débranche ensuite le condensateur de la batterie, mais le condensateur reste chargé. On double ensuite la distance entre les plaques. Quelle est maintenant l’énergie dans le condensateur ?
7.6 Les circuits avec des résistances et des condensateurs
24. Dans le circuit RC suivant, combien faudra-t-il de temps après la fermeture de l’interrupteur pour que le condensateur ait 90 % de sa charge maximale ?
25. Dans le circuit suivant, le courant diminue à 50 % de sa valeur initiale en 5 ms après la fermeture de l’interrupteur. Quelle est la capacité du condensateur ?
26. Voici un circuit RC.
a) Quel est le courant initial dans la résistance quand on ferme l’interrupteur ?
b) Quel est le courant dans la résistance 90 secondes après la fermeture de l’interrupteur ?

c) Quelle est la puissance dissipée par la résistance 90 secondes après la fermeture de l’interrupteur ?
d) Quelle est la charge du condensateur 90 secondes après la fermeture de l’interrupteur ?
e) Quelle est la différence de potentiel aux bornes du condensateur 90 secondes après la fermeture de l’interrupteur ?
f) Quelle est la différence de potentiel aux bornes de la résistance 90 secondes après la fermeture de l’interrupteur ?
g) Quelle est l’énergie dans le condensateur 90 secondes après la fermeture de l’interrupteur ?
h) Quelle est l’énergie dissipée en chaleur par la résistance durant les premières 90 secondes après la fermeture de l’interrupteur ?
27. Un condensateur de 20 mF ayant initialement une charge de 4 C se décharge à travers une résistance de 10 000 Ω.
a) Quel est le courant initial dans la résistance quand on ferme l’interrupteur ?
b) Quel est le courant dans la résistance 90 secondes après la fermeture de l’interrupteur ?
c) Quelle est la puissance dissipée par la résistance 90 secondes après la fermeture de l’interrupteur ?
d) Quelle est la charge du condensateur 90 secondes après la fermeture de l’interrupteur ?

e) Quelle est l’énergie initiale dans le condensateur ?
f) Quelle est l’énergie dans le condensateur 90 secondes après la fermeture de l’interrupteur ?
g) Quelle est l’énergie dissipée en chaleur par la résistance durant les premières 90 secondes après la fermeture de l’interrupteur ?
28. Dans le circuit suivant, quel est le courant fourni par la pile 120 secondes après la fermeture de l’interrupteur ?
29. On a le circuit suivant.
a) Quelle sera la valeur maximale indiquée par l’ampèremètre après la fermeture de l’interrupteur ?
b) Combien faudra-t-il de temps pour que le courant indiqué par l’ampèremètre diminue à 1 A ?
30. Quand un condensateur se vide à travers une résistance, il faut 0,5 seconde pour que le courant descende à 50 % de sa valeur initiale. Combien faudra-t-il de temps pour que le courant ne soit plus que 1 % de sa valeur initiale ?
31. Dans le circuit suivant, on ferme l’interrupteur très longtemps, puis on l’ouvre.
Quelle sera la charge du condensateur 20 secondes après l’ouverture de l’interrupteur ?
32. Voici un circuit avec des résistances et un condensateur.

a) Quel est le courant fourni par la source immédiatement après la fermeture de l’interrupteur ?
b) Quel est le courant fourni par la source longtemps après la fermeture de l’interrupteur ?
c) Quelle est la charge du condensateur longtemps après la fermeture de l’interrupteur ?
7.7 Les diélectriques
33. Voici un condensateur à plaque parallèle.
a) Quelle est la capacité de ce condensateur ?
b) Quelle est l’énergie maximale que peut emmagasiner ce condensateur ?
34. Quelle est la capacité de ce condensateur cylindrique ?
35. Les plaques de ce condensateur à plaque parallèle ont une aire de 90 cm². Quelle est la capacité de ce condensateur ?
36. Les plaques de ce condensateur à plaque parallèle ont une aire de 90 cm². Quelle est la capacité de ce condensateur ?
37. Quelle est la capacité de ce condensateur ?
38. On charge un condensateur de 12 µF avec une source de 24 V. On débranche ensuite la source et on introduit ensuite un diélectrique entre les plaques. Ce diélectrique a une permittivité relative de 3 et il occupe tout l’espace entre les plaques. Quelles sont les valeurs de la charge des plaques et de la différence de potentiel entre les plaques après qu’on ait introduit le diélectrique ?

39. On charge un condensateur de 12 µF avec une source de 24 V. On introduit ensuite un diélectrique entre les plaques tout en laissant le condensateur branché à la source. Ce diélectrique a une permittivité relative de 3 et il occupe tout l’espace entre les plaques. Quelles sont les valeurs de la charge des plaques et de la différence de potentiel entre les plaques après qu’on ait introduit le diélectrique ?
40. Comment change la charge du condensateur du bas dans ce circuit quand on introduit un diélectrique ayant une constante de k = 12 entre les armatures du condensateur ? La capacité du condensateur est de 20 µF avant l’introduction du diélectrique.
41. Ce condensateur à plaque parallèle est rempli d’un diélectrique. Or, ce diélectrique conduit l’électricité, ce qui fait que le condensateur se décharge lentement à travers le diélectrique. Au bout de combien de temps le condensateur aura-t-il perdu la moitié de se charge initiale ?
7.2 La capacité
1. 88,54 pF
2. a) 13,91 pF b) 1,391 nC c) 5000 N/C
3. 66,76 nF
4. a) 2,288 pF b) 437,1 V
5. 18,37 cm
6. 4,427 mm
7.3 Circuits simples avec des condensateurs
7.
8.

9. a) condensateur de 20 µF : 480 µC condensateur de 30 µF : 720 µC b) 24 V
10. a) condensateur de 40 µF : 2000 µC condensateur de 20 µF : 1000 µC b) 50 V
11. 25 µF
12. La différence de potentiel reste la même (12 V) et la charge baisse de 324 µC
13. La charge reste la même (432 µC) et la différence de potentiel monte de 36 V 14.
15. 50 µC
7.4 Les condensateurs en série et en parallèle
16. 13,625 µF 17.
18.
19. a) 24 µF b) 1,5 V
7.5 L’énergie dans un condensateur
20. 0,4 J
21. 2,214 µm

22. Condensateur de 12 µF : 9,6 x 10-5 J
Condensateur de 6 µF : 1,92 x 10-4 J
Condensateur de 4 µF : 2,88 x 10-4 J
23. 0,24 J
7.7 Les circuits avec des résistances et des condensateurs
24. 115,1 s
25. 3,607 µF
26. a) 4,8 mA b) 3,833 mA c) 0,07345 W d) 0,3868 C e) 4,836 V
f) 19,164 V g) 0,9353 J h) 8,349 J
27. a) 20 mA b) 12,75 mA c) 1,626 W d) 2,551 C e) 400 J f) 162,6 J g) 237,4 J
28. 2,475 mA
29. a) 6 A b) 6,163 ns

30. 3,322 s
31. 1,213 C
32. a) 16,8 A b) 15 A c) 118,8 µC
7.7 Les diélectriques
33. a) 885,4 pF b) 1,02 J
34. 96,31 pF
35. 106,25 pF
36. 91,95 pF
37. 566,7 pF
38. La charge reste la même à 288 µC et la différence de potentiel diminue à 8 V
39. La différence de potentiel reste la même à 24 V et la charge augmente à 864 µC
40. La charge passe de 180 µC à 576 µC.

41. 920,6 s
